💧🌏 Greg CocksAug 27
Favorability Mapping For Hydrothermal Power Resource Assessments Of The Great Basin, USA
--
https://doi.org/10.1016/j.geothermics.2025.103450 <-- shared paper
--
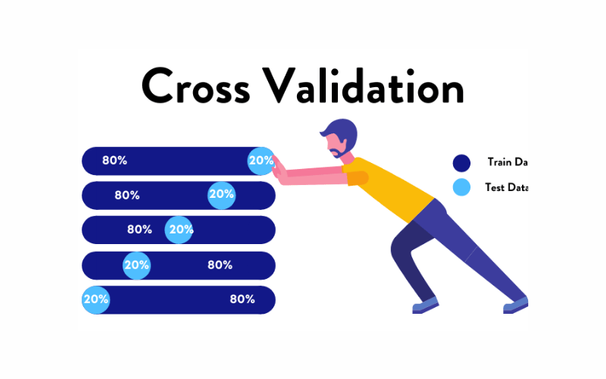
#geothermal #resourceassessment #hydrothermal #favorability #GreatBasin #datadriven #Machinelearning #ML #AI #USA #power #energy #powerplant #renewableenergy #survey #spatialanalysis #GIS #spatial #mapping #montecarlo #model #modeling #crossvalidation #predication #WesternUSA #algorithm #training #geology #vulcanism #favorability #research #prospecting #resources
#USGS
nf-coreJul 3

Pipeline release! nf-core/drugresponseeval v1.1.0 - Drugresponseeval 1.1.0 - Humongous Zapdos!

Please see the changelog: https://github.com/nf-core/drugresponseeval/releases/tag/1.1.0

#celllines #crossvalidation #deeplearning #drugresponse #drugresponseprediction #drugs #fairprinciples #generalization #hyperparametertuning #machinelearning #randomizationtests #robustnessassessment #training #nfcore #openscience #nextflow #bioinformatics

Release Drugresponseeval 1.1.0 - Humongous Zapdos · nf-core/drugresponseeval

What's Changed Added #43 Preprint is out now! Linking it in the documentation. #42 Added authors and licenses to the python scripts. #43 Added --no_hyperparameter_tuning flag for quick runs withou...

GitHub
HabrJul 3

Кросс-валидация на временных рядах: как не перемешать время

Привет, Хабр! Сегодня рассмотрим то, что чаще всего ломает даже круто выглядящие модели при работе с временными рядами — неправильная кросс‑валидация . Разберем, почему KFold тут не работает, как легко словить утечку будущего, какие сплиттеры реально честны по отношению ко времени, как валидировать фичи с лагами и агрегатами.

https://habr.com/ru/companies/otus/articles/921604/

#временные_ряды #time_series #машинное_обучение #прогнозирование #кроссвалидация #crossvalidation

Кросс-валидация на временных рядах: как не перемешать время

Привет, Хабр! Сегодня рассмотрим то, что чаще всего ломает даже круто выглядящие модели при работе с временными рядами — неправильная кросс-валидация . Разберем, почему KFold тут не работает, как...

Хабр
InterData VNMay 3

Cross-Validation là gì trong Machine Learning? A-Z

Cross-Validation là một kỹ thuật then chốt trong Machine Learning, giúp kiểm tra hiệu suất và khả năng tổng quát của mô hình trên dữ liệu mới. Nhờ đó, mô hình tránh được tình trạng học lệch và hoạt động ổn định hơn. Bài viết này sẽ cùng bạn khám phá chi tiết về Cross-Validation, lý do nó quan trọng và các phương pháp xác thực phổ biến hiện nay.

Xem chi tiết bài viết tại đây: https://interdata.vn/blog/cross-validation-la-gi/

#interdata #crossvalidation

neuralrowFeb 28

New article out folks
Check it out
https://medium.com/@neuralrow/cross-validation-1df416898697

#DataScience #MachineLearning #CrossValidation #LinearRegression #DeepLearning #NeuralNetworks

Guide to Cross-Validation in Machine Learning - NeuralRow - Medium

The basic idea of cross-validation is to split the data first into training and test parts. Then, the training part is further divided into subtrain and validation parts, cycling through these…

Medium
nf-coreJan 31

Pipeline release! nf-core/drugresponseeval v1.0.0 - 1.0.0!

Please see the changelog: https://github.com/nf-core/drugresponseeval/releases/tag/1.0.0

#celllines #crossvalidation #deeplearning #drugresponse #drugresponseprediction #drugs #fairprinciples #generalization #hyperparametertuning #machinelearning #randomizationtests #robustnessassessment #training #nfcore #openscience #nextflow #bioinformatics

Release 1.0.0 · nf-core/drugresponseeval

What's Changed Important! Template update for nf-core/tools v3.0.1 by @nf-core-bot in #10 Merge branch 'dev' of github.com:nf-core/drugresponseeval into dev by @JudithBernett in #11 Global checkpo...

GitHub
Dr Mircea Zloteanu 🍁 🍃May 29, 2024

#statstab #103 On the marginal likelihood and cross-validation

Thoughts: Can't say I can follow much of this, so I'll open it up to the #bayesian community for input. Seems important though.

#stats #bayes #likelihood #evidence #crossvalidation

https://doi.org/10.1093/biomet/asz077

On the marginal likelihood and cross-validation

Summary. In Bayesian statistics, the marginal likelihood, also known as the evidence, is used to evaluate model fit as it quantifies the joint probability

OUP Academic
Show threadChloé AzencottMay 29, 2024

⬆️

6) thankfully, Wager (2020) https://doi.org/10.1080/01621459.2020.1727235 shows that cross-validation is asymptotically consistant for model selection, so while what we're doing gives us poor estimates of generalization error and bad error bars, at least it's valid for model selection.

#machineLearning #statistics #crossValidation

Show threadChloé AzencottMay 29, 2024

⬆️

5) Bates et al. (2023) https://doi.org/10.1080/01621459.2023.2197686 propose a nested cross-validation estimator of generalization error that's unbiased and has an unbiased mean squared error estimator. It's computationally quite intensive. I played a bit with it, and my in high-dimensional set ups (large p small n) I got error bars that had indeed good coverage of the generalization error, but were also covering most of the [0, 1] interval, which is less helpful.

⬇️

#machineLearning #statistics #crossValidation

Show threadChloé AzencottMay 29, 2024

⬆️

4) in any case, error bars are wrong, because it's impossible to get an unbiased estimator of the mean squared error of an estimator that's based on a single fold of cross-validation, as shown by Bengio & Grandvalet (2004) https://dl.acm.org/doi/10.5555/1005332.1044695

⬇️

#machineLearning #statistics #crossValidation

No Unbiased Estimator of the Variance of K-Fold Cross-Validation | The Journal of Machine Learning Research

Most machine learning researchers perform quantitative experiments to estimate generalization error and compare the performance of different algorithms (in particular, their proposed algorithm). In order to be able to draw statistically convincing ...

The Journal of Machine Learning Research