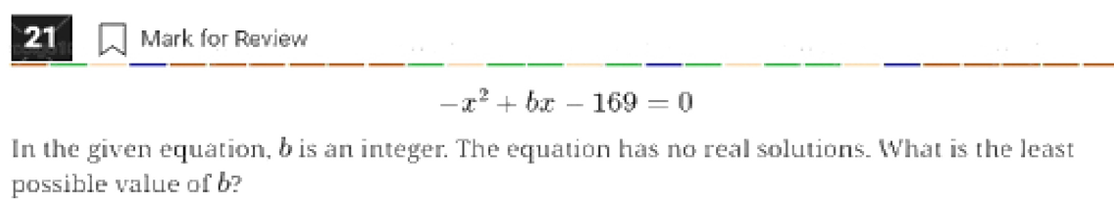Giuseppe MichieliMurine #betacoronavirus #spike protein: A major #determinant of #neuropathogenic properties, https://etidiohnew.blogspot.com/2025/03/murine-betacoronavirus-spike-protein.html
Aatubeimpossible
impossible #math #sat #quadratic #determinant
ƧƿѦςɛ♏ѦਹѤʞWhat Numbers Do You Get by Iteratively Scaling a Matrix?
https://www.youtube.com/watch?v=-uIwboK4nwE
#maths #mathematics #Sinkhorn #matrix #determinant #scaling #math
https://www.youtube.com/watch?v=-uIwboK4nwE
#maths #mathematics #Sinkhorn #matrix #determinant #scaling #math
What Numbers Do You Get by Iteratively Scaling a Matrix?
Eric MaugendreFor all Transf ∈ ℝn×n, the matrix is invertible if and only if rank(Transf) = n
The #determinant exists if and only if the transformation matrix is square.
The determinant in a linear transformation is the (signed) area of the image of the fundamental basis formed by the unit square.
#algebra #matrices #tutorial #determinants #singularity #math #maths #mathematics #mathStodon #ML #machineLearning #systems
Mathieu GouxYeah o/ Mon premier article en anglais, co-écrit avec un collègue, est paru aujourd'hui dans le "Journal of French Language Studies" ! Je suis joie :) Ça parle de corpus, de déterminants, d'histoire du français et y'a, genre whatmille tableaux. Yeah :D
#Linguistics #Linguistique #Grammaire #Déterminant #LangueFrançaise
Markus RedekerWhy is the determinant of the matrix \( \begin{pmatrix} a_1 & b_1 \\ a_2 & b_2 \end{pmatrix} \) equal to \( a_1 b_2 - a_2 b_1 \)?
I have found a geometrical interpretation (https://functor.network/user/414/entry/299) and with it also started a blog.
#WordsAndSomeFormulas #Mathematics #MathEdu #Determinant #Geometry
King BeauregardDETERMINANTS AND THE BAREISS ALGORITHM
If you have to calculate determinants, and especially if you have to program an algorithm, investigate the Bareiss algorithm. It's remarkably fast; it limits the divisions so that it doesn't introduce needless rounding errors; and if your matrix elements are all integers, Bareiss is guaranteed to give you an integer result.
I've worked out a way to do Bareiss on pen and paper; here's a link to a PDF showing the technique:
sibakuHm... I think I will do a little visual intuition #LiaScript doc about the determinant and how it corresponds to area/volume 🤔 I feel that many people are very confused by the #determinant when they encounter it in a linear algebra #math class. At least in mine, it was this weird abstract function (granted, this way of going about things also has its positives), not like a geometric thing. Then you see it popping up in like multivariate integrals with volume elements and its like... huh?
Marek GluzaI'm reading Artin's #GaloisTheory and I'm wondering if the #math exposition of the #matrix #determinant relying on homogeneity properties is related to the #BrunnMinkowski #inequality
I will check my handwritten notes when I'll be in Poland end of July but I remember that homogeneity played a role there.
This rambling is related to my struggle to understand the #BrascampLieb and #rearrangementInequality. Any hints much appreciated 🥹😅🙈😊
Joshua GrochowIs there an "addition function" that works simultaneously for the determinant and the permanent?
#complexity #permanent #determinant
There is a simple function that is multiplicative for both the determinant and permanent simultaneously, namely \(\det(A \oplus B) = \det(A)\det(B)\) and \(perm(A \oplus B)=perm(A)perm(B)\).
The map \(A,B \mapsto A \oplus B\) is a projection in Valiant's sense - every coordinate of the output is either one of the input coordinates or a constant.
Perm and det both have "addition functions" separately. They are slightly more complicated, but still projections. That is, there are projections f,g such that det(f(A,B))=det(A) + det(B) [Malod & Portier, Prop 7 https://doi.org/10.1016/j.jco.2006.09.006] and perm(g(A,B)) = perm(A) + perm(B) [see https://cstheory.stackexchange.com/a/51348/129].
But is there a single projection h such that
det(h(A,B)) = det(A) + det(B)
and
perm(h(A,B)) = perm(A) + perm(B)
?
I don't know, but would love to find out!