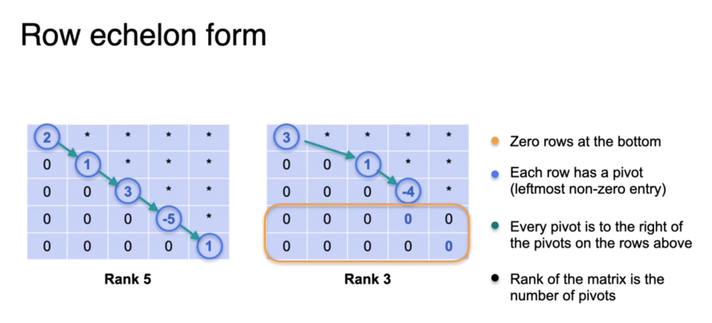
A system (of sentences, of equations, of graphs) is said "complete" if it has one and only one solution.
A system is deemed "singular" if it does not have one and only one solution.
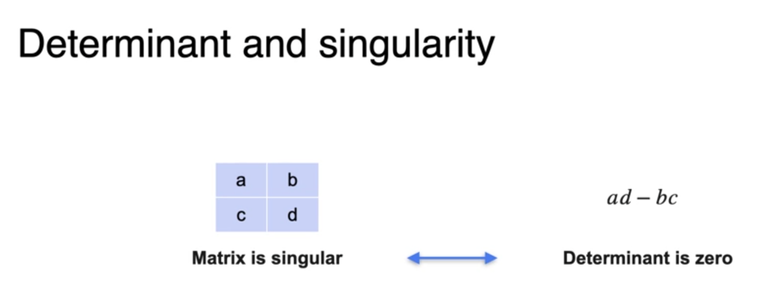
A convenient way to show singularity is to:
* define a "determinant" as the product of the leading diagonal minus the product of the antidiagonal and
* calculate that it is zero.
#learning #algebra #systems #matrices #determinants #singularity #data #ML #DataScience #math #maths #mathematics #tutorial
Linear algebra (continued)
Which of the below operations, when applied to the rows of a matrix, keeps the #singularity (or non-singularity) of the matrix?:
(Hint: It works the same as a system of linear equations.)
#learning #algebra #systems #matrices #determinants #singularity #data #ML #DataScience #math #maths #mathematics #mathStodon #tutorial #poll #exercise #exercice #puzzle #calculus
Operations that keep #matrix singularity :
v Adding one row to another one.
Correct: Adding two rows is equivalent to adding two equations in a system of equations.
v Switching rows.
Correct: Switching rows is equivalent to switching equations in a system of equations.
v Multiplying a row by a nonzero scalar.
Correct: Multiplying a row by a nonzero scalar is equivalent to scaling a whole equation.
_ Adding a nonzero number to every entry of the row.
False!
Next instalment: #rank of a matrix
To simplify linear #systems, we may code #elimination: We construct a matrix with the conditions:
* Rows consisting entirely of zeros should be positioned at the bottom.
* Each non-zero row must have its left-most non-zero coefficient (called #pivot) located to the right of any row above it.
A system is invertible if and only if there are no zeros in the leading diagonal of this "Row echelon form".
For compressing images, we use the #rank of a matrix: the number of "pivots" in the matrix:
Data returned by an observation typically is represented as a vector in machine learning.
A neural network can be seen as a large collection of linear models. We may represent the inputs and outputs of each layer as vectors, matrices, and tensors (which are like higher dimensional matrices).
#algebra #linearAlgebra #vectors #matrices #determinants #singularity #ML #DataScience #math #maths #mathematics #mathStodon #ML #data #dataDon #dataScience #machineLearning #DeepLearning #neuralNetworks
Let's assume a vector is u, then:
The vectors that have #dotProducts of 0 with u are all the perpendicular vectors to u.
The vectors that have a positive dot product with u are all the vectors in u's semi-space.
The vectors that have a negative dot product with u are in the complementary region.
The product of a matrix and a vector is the dot products stacked together.
We can have a system of four equations and three unknown variables, and on the right, we have four dot products stacked:
#Algebra thread ๐งต
Which #matrices have an inverse?
Singular matrices never have an inverse.
When we look at the determinant, the determinant is non-zero for invertible matrices in the same way that non-zero numbers have an inverse.
Non-zero determinants mean that the matrices has an inverse, and a zero determinant means that the system (of sentences, of graphs) is singular.
#tutorial #learning #determinants #singularity #math #maths #mathematics #mathStodon #ML #machineLearning #systems
For all Transf โ โnรn, the matrix is invertible if and only if rank(Transf) = n
The #determinant exists if and only if the transformation matrix is square.
The determinant in a linear transformation is the (signed) area of the image of the fundamental basis formed by the unit square.
#algebra #matrices #tutorial #determinants #singularity #math #maths #mathematics #mathStodon #ML #machineLearning #systems
The #span of a set of k #vectors is the collection of all their linear combinations.
In other words, the span of ๐ฃ1,๐ฃ2,โฆ,๐ฃk consists of all the vectors b for which the equation [๐ฃ1๐ฃ2โฆ๐ฃk]x=b is consistent.
Beware: The dimension of a vector space is not necessarily the number of elements in a vector. ๐ = span( [1 0.5] ) is one-dimensional.
A set of vectors is linearly independent if and only if the vectors form a matrix that has a pivot in every column.
Eric Maugendre