https://www.viennot.org/abjc.html #bijectivecombinatorics #hackernews #writinghumor #mathcomedy #HackerNews #ngated
https://www.viennot.org/abjc.html #bijectivecombinatorics #hackernews #writinghumor #mathcomedy #HackerNews #ngated
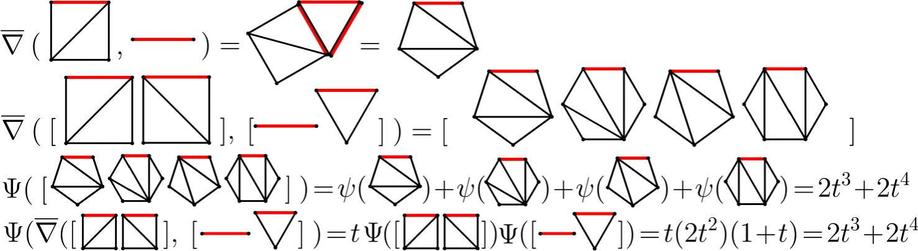
The Art of Bijective Combinatorics
https://www.viennot.org/abjc.html
#HackerNews #BijectiveCombinatorics #Combinatorics #Art #Mathematics #MathEducation
Maypole Dance of Braid Like Groups
https://divisbyzero.com/2009/05/04/the-maypole-braid-group/
#HackerNews #Maypole #Dance #Braid #Groups #Mathematics #Combinatorics #HackerNews
Just yesterday, I was musing to a (younger) research visitor, "I hope that within my lifetime we will still see another breakthrough on the bounds for R(3,k)"...
https://arxiv.org/abs/2505.13371
I am excited to see what developments follow on from here!
(Also that old adage: just as soon as you publish a survey (https://arxiv.org/abs/2501.03379) it is out of date.)
#math #mathematics #combinatorics #ExtremalCombinatorics #graphtheory #probability

A new lower bound for the Ramsey numbers $R(3,k)$
We prove a new lower bound for the off-diagonal Ramsey numbers, \[ R(3,k) \geq \bigg( \frac{1}{3}+ o(1) \bigg) \frac{k^2}{\log k }\, , \] thereby narrowing the gap between the upper and lower bounds to a factor of $3+o(1)$. This improves the best known lower bound of $(1/4+o(1))k^2/\log k$ due, independently, to Bohman and Keevash, and Fiz Pontiveros, Griffiths and Morris, resulting from their celebrated analysis of the triangle-free process. As a consequence, we disprove a conjecture of Fiz Pontiveros, Griffiths and Morris that the constant $1/4$ is sharp.
Day 1 of #Integers2025 just wrapped up! Integers is a #NumberTheory and #Combinatorics conference. There's historically a bit of CGT too. Here are my summaries of the #CombinatorialGames talks: https://combinatorialgametheory.blogspot.com/2025/05/integers-2025-cgt-talks.html
Two of the talks were the result of #UndergraduateResearch!
(Just finished writing my laudatio speech.)
Eoin Hurley will defend his PhD on Wednesday.
#combinatorics #graphtheory #ExtremalCombinatorics #probability #algorithms #math
Astonishing! I hadn't come across this before - absolutely fascinating!
#maths #mathematics #polynomial #polynomials #CatalanNumbers #combinatorics #Galois #GaloisTheory
https://www.tandfonline.com/doi/epdf/10.1080/00029890.2025.2460966?needAccess=true
I'm going crazy trying to figure out this paper.
In Wildberger & Rubine’s 2025 paper linked below (DOI:10.1080/00029890.2025.2460966), where is the explicit combinatorial formula or recurrence for the one‑variable Geode coefficients Gₖ given? I'm dying here.
I'd like to understand the method, but this is a huge roadblock.
EDIT: Issue is solved (yet funny enough, unsolved)
#math #algebra #combinatorics #galois #mathresearch #powerseries
https://www.tandfonline.com/doi/full/10.1080/00029890.2025.2460966#d1e7853
As part of the Sparse (Graphs) Coalition (https://sparse-graphs.mimuw.edu.pl/doku.php?id=start), there will be a "Café" session:
https://sparse-graphs.mimuw.edu.pl/doku.php?id=sessions:2025sessions:2025cafesession1
We will host an online panel discussion related to the question, "How can we make the most of computer-aided methods in mathematics/combinatorics?"
#openscience #researchpractices #graphs #combinatorics #math
Meta's Llama 4 (which is being forced on all #WhatsApp users) doesn't do any of chain-of-thought reasoning and incorrectly calculates the number of squares of one colour. Claims that a 7x7 checker board with one corner missing has 23 of one colour so makes tiling impossible but then continues on for several paragraphs about possible tiling approaches.