As 3D generative AI matures, it’s reshaping creativity across multiple disciplines.
This year, ever-expanding work in the 3D generative AI space will be explored as part of the SIGGRAPH Technical Papers program, including these three novel methods — each offering a unique take on how 3D generative AI is being applied.
Check out the award-winning research here: https://blog.siggraph.org/2025/06/siggraph-2025-technical-papers-awards-best-papers-honorable-mentions-and-test-of-time.html/
#SIGGRAPH2025 #TechnicalPapers #Research #ComputerGraphics
Breakthrough ideas start here.
The SIGGRAPH 2025 Technical Papers program showcases the latest innovations in computer graphics and interactive techniques.
Check it out: https://www.youtube.com/watch?v=HfHC0wNYry8&t=8s
When: August 10–14, 2025
Where: Vancouver, Canada
#SIGGRAPH2025 #TechnicalPapers #Research #ComputerGraphics
It's crazy how advanced the graphics software on Symbolics LISP machines were in the 1980's before SGI kind of took over that space.
#Retrocomputing #LispMachine #ComputerGraphics
Interesting video: "Inside The Witcher 4 Unreal Engine 5 Tech Demo: CD Projekt RED + Epic Deep Dive Interview" https://www.youtube.com/watch?v=OplYN2MMI4Q
#gamedev #gameart #computergraphics

Inside The Witcher 4 Unreal Engine 5 Tech Demo: CD Projekt RED + Epic Deep Dive Interview
Vcc - the Vulkan Clang Compiler
https://lemmy.ml/post/31246365
Vcc - the Vulkan Clang Compiler - Lemmy
cross-posted from: https://lemmy.ml/post/31246361
[https://lemmy.ml/post/31246361] > Vcc - the Vulkan Clang Compiler, is a
proof-of-concept C and C++ compiler for Vulkan leveraging Clang as a front-end,
and Shady our own research IR and compiler. Unlike other shading languages, Vcc
aims to stick closely to standard C/C++ languages and merely adds a few new
intrinsics to cover GPU features. Vcc is similar to CUDA or Metal in this
regard, and aims to bring the advantages of standard host languages to Vulkan
shaders. > > Key Features > > Vcc supports advanced C/C++ features usually left
out of shading languages such as HLSL or GLSL, in particular raising the bar
when it comes to pointer support and control-flow: > > - Unrestricted pointers >
- Arithmetic is legal, they can be bitcasted to and from integers > - Generic
pointers > - Generic pointers do not have an address space in their type, rather
they carry the address space as a tag in the upper bits. > - True function calls
> - Including recursion, a stack is implemented to handle this in the general
case > - Function pointers > - Lets you write code in a functional style on the
GPU without limitations > - Arbitrary goto statements - code does not need to be
strictly structured ! > > Many of these capabilities are present in compute
APIs, but are not supported in most graphics APIs such as DirectX or Vulkan. We
aim to address this gap by proving these features can and should be implemented.
More on why we think that’s important.

Rendering 'Assassin's Creed Shadows'
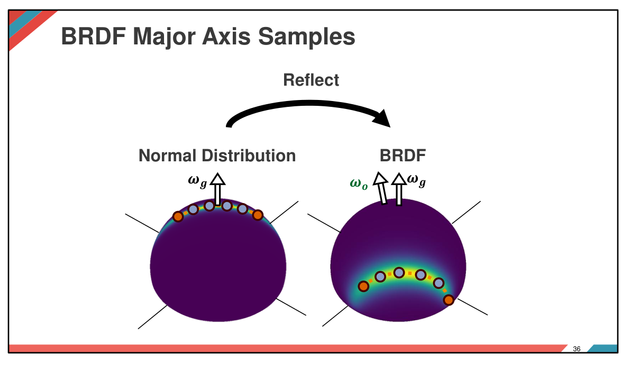
Curious about sampling the major axis of a specular GGX BRDF for image-based lighting? 📸💡
Check out these slides: https://drive.google.com/file/d/1BkFt4dmwM6w4N0cFWnANLJLyIAPIdKJC/view?usp=sharing
#ComputerGraphics #Rendering #IBL