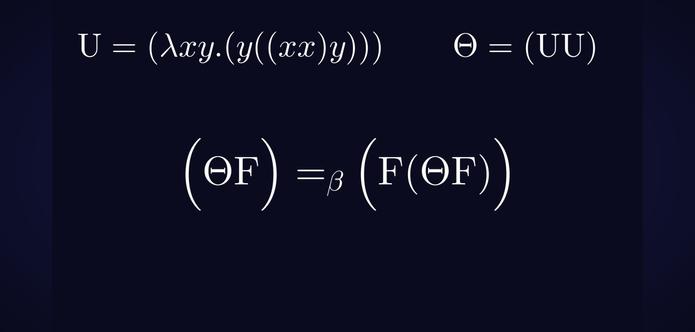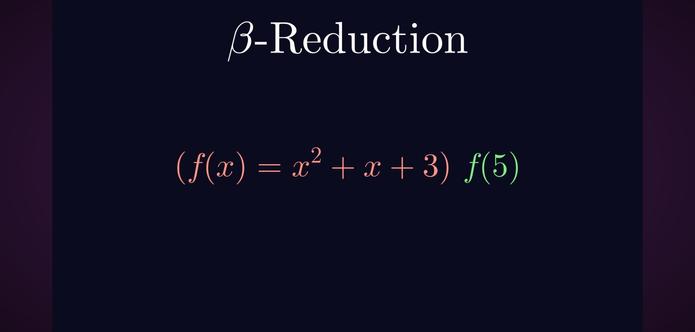Will Berard 🫳🎤🫶TFW playing Functional
N-gated Hacker News🤓💻 Oh goody, another article assuming we all have Ph.D.s in Lambda Calculus! 🙄 De Bruijn might be useful, but unless you're a sentient textbook, this read is a snooze. 💤✨
https://blueberrywren.dev/blog/debruijn-explanation/ #LambdaCalculus #SnoozeFest #SentientTextbook #DeBruijn #TechHumor #ProgrammerLife #HackerNews #ngated
https://blueberrywren.dev/blog/debruijn-explanation/ #LambdaCalculus #SnoozeFest #SentientTextbook #DeBruijn #TechHumor #ProgrammerLife #HackerNews #ngated
Artyom Bologov@neauoire inspired me with their idea of a #UXN book and I wondered what my book might be about. And then I realized! I already have a series of #blogpost-s about #LambdaCalculus, so I can just continue that and I'll have a book! Intention in place, I set to continue my gargantuan series of "Making Sense of Lambda Calculus" posts. So here's a (0-indexed) part 5, "Bring Computation to (Aggregate) Data":
https://aartaka.me/lambda-5.html
@amoroso @bouncepaw did you two read the previous episodes? How were they?
So I watched this video https://www.youtube.com/watch?v=RcVA8Nj6HEo
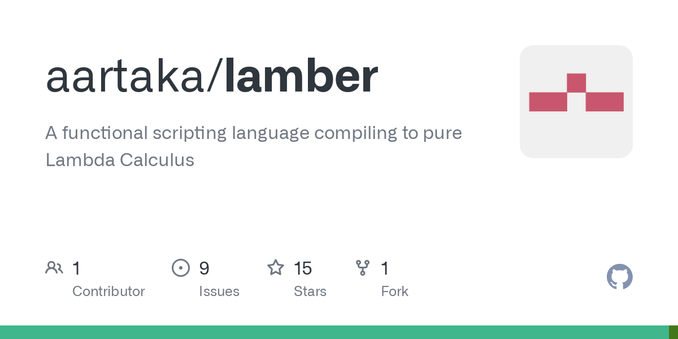
And I decided to check what "plus times plus" actually computes. Luckily, I have my own #LambdaCalculus compiling language, #Lamber f https://github.com/aartaka/lamber
So I ran "* + + 1 2 3" and got... 36. So a number from a #math operator applied to other operators and then to data. Which seems like a nice basis for math conspiracy theories. How many of the basic arithmetic functions can we combine, and to what result? Might even end up with lambda calculus #codegolf things, like this division function John Tromp listed with attribution to Bertram Felgenhauer:
def div fn (dividend divisor)
local F = fn (m f t)
m T' (fn (c) f : c t) id .
int (fn (f x)
(int dividend) T' (K x) ((int dividend) (F (int divisor) f) x)) .
Adapted to Lamber, of course. But not any more readable than it used to be. Which is a cool feature of LC—you can apply anything to anything and get something as a result, albeit with a really confusing program flow.
I'm that close to learning some logical language and trying to devise mine, with lambda diagrams as concept ideograms and function application as the only syntactic relation. Yeah I know I'm going crazy, but at least it's fun.
What is PLUS times PLUS?
Light
Christian TietzeI believe I may have found a way to describe #zettelkasten work in #lambdacalculus — like, what it entails to do something in your Zettelkasten, and the communication system that emerges
Lamber, my #LambdaCalculus -> Lisp compiler (https://github.com/aartaka/lamber) didn't handle big enough numbers (> 10-bit,) so I decided to implement some optimizations, reusing underlying #CommonLisp compiler to speed up and save space on numerics. It's not particularly reliable, because big LC numbers consume too much of the stack, but at least it's better than it used to be, almost reliably handling 12-bit numbers.
coucouWhat is PLUS times PLUS?
HoldMyType#python lets ypu instantiate a function anywhere and a ( recursive) function definition can be self contained and last i checked its notorious for its type checking
#Lambdacalculus wont let you do that unyil you give it the required fixed point function
#typetheory
Oh and fixed point need not be in R
Unlike rieman zeta ?
OTOH python wont spit potential Nonsense
#Lambdacalculus wont let you do that unyil you give it the required fixed point function
#typetheory
Oh and fixed point need not be in R
Unlike rieman zeta ?
OTOH python wont spit potential Nonsense
term Q = λ1((λ11)(λλλλλ14(3(55)2)))1 concatenates two copies of its input, proving that
KS(xx) ≤ ℓ(x) + 66Applying it to its own encoding gives a 132 bit quine:
U(blc(Q) blc(Q) : Nil) = blc(Q) blc(Q)
#lambdacalculus
https://tromp.github.io/cl/Binary_lambda_calculus.html
