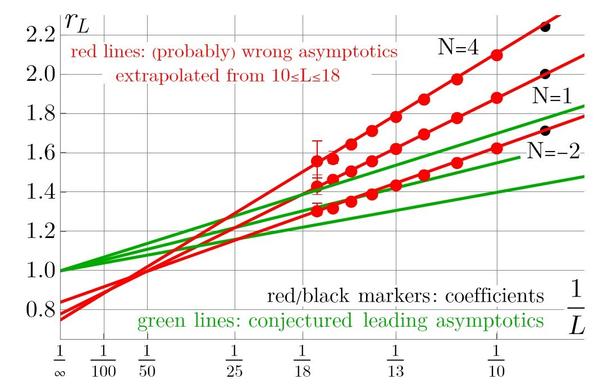
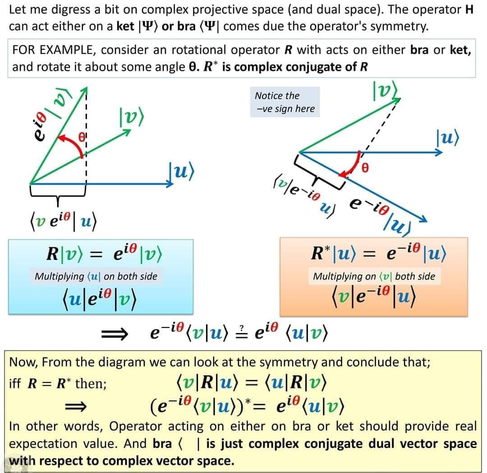
Two years ago, I began writing my
#doctoralThesis in theoretical
#physics. Most effort went into giving a very detailed pedagogical account of what the
#renormalization #HopfAlgebra in
#QuantumFieldTheory does, and why it is natural and transparent from a physical perspective.
One year ago, my referees recommended in their reports to publish the thesis as a book, and today I received the printed copies!
It was exciting to go through all the steps of actually publishing a book, and I hope that it will be of use to convince physicists that the Hopf algebra structure in
#QFT is not a weird mathematical conundrum, but it actually encodes the very way physicists have been thinking of renormalization since the 1950s: Parametrize a theory by quantities one can actually measure, instead of fictional expansion parameters.
https://link.springer.com/book/10.1007/978-3-031-54446-0