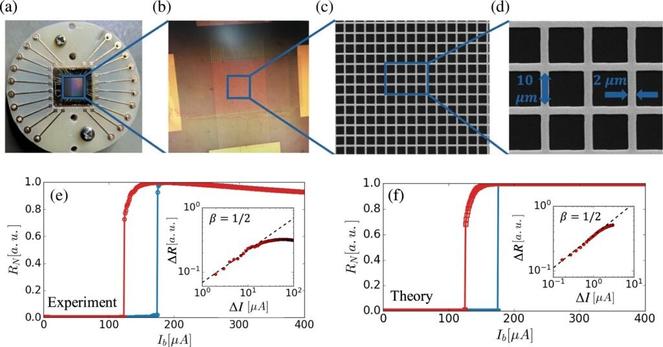
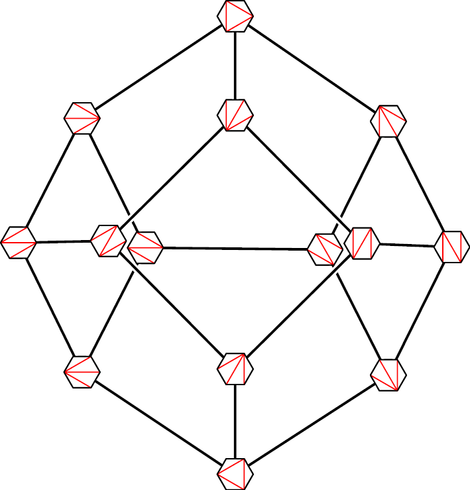
This shape is the 3d associahedron.
To get it, take a hexagon and triangulate it by drawing red lines between its corners - lines that don't cross each other. There are 14 ways to do this, and these are the vertices of the associahedron. You get an edge of the associahedron from two triangulations that have two red lines in common. You get a face from all the triangulations that have one red line in common.
If you replace the hexagon by a polygon with more sides, you get a higher-dimensional associahedron. The associahedra have many magical properties, and here's one of the most astounding.
Take a formal power series like this:
𝐶(𝑥) = 𝑥 + 𝑐₁𝑥² + 𝑐₂𝑥³ + ⋯
If you take its inverse under composition, meaning the power series 𝐷 with
𝐶(𝐷(𝑥)) = 𝑥
you get another formal power series of the same type:
𝐷(𝑥) = 𝑥 + 𝑑₁𝑥² +𝑑₂𝑥³ + ⋯
How are the numbers 𝑑ₙ related to the numbers 𝑐ₙ? Do some calculations:
𝑑₁ = −𝑐₁
𝑑₂ = −𝑐₂ + 2𝑐₁²
𝑑₃ = −𝑐₃ + 5𝑐₂𝑐₁ − 5𝑐₁³
𝑑₄ =−𝑐₄ + 6𝑐₃𝑐₁ + 3𝑐₂² − 21𝑐₂𝑐₁² + 14𝑐₁⁴
What are these coefficients? They're controlled by the associahedra! I'll show how it works for 𝑑₄.
Call the n-dimensional associahedron 𝑐ₙ₋₁, so that 𝑐₁ is a point, 𝑐₂ is an interval, 𝑐₃ is a pentagon, and so on. From the picture notice that the 3d associahedron 𝑐₄ has
• 1 face shaped like 𝑐₄ (the whole thing)
• 6 faces shaped like 𝑐₃ × 𝑐₁ (pentagons) and 3 faces shaped like 𝑐₂ × 𝑐₂ (squares)
• 21 faces shaped like 𝑐₂ × 𝑐₁× 𝑐₁ (the edges)
• 14 faces shaped like 𝑐₁ × 𝑐₁ × 𝑐₁ × 𝑐₁ (the vertices)
All this information is packed into here:
𝑑₄ = −𝑐₄ + 6𝑐₃𝑐₁ + 3𝑐₂² − 21𝑐₂𝑐₁² + 14𝑐₁⁴
Look at it!
We get the other 𝑑ₙ from the associahedra of other dimensions, in the same way!
(1/2)
UK
Metin Seven 🎨
John Carlos Baez
Rxiv mechanobio
Андрей
franco_vazza