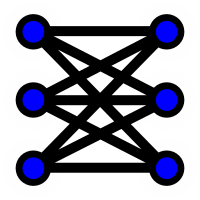
Polyomino "fence" problems ask you to maximize the area surrounded by a set of polyominoes. I usually don't find these problems terribly interesting, but in this case I was looking at a piece set that didn't seem to want to do much else.

The base piece set here is the polyominoes with perimeter 10. Doing anything novel with matched polyomino edge markings is tough. First, Peter Esser has probably already done it: https://polyforms.eu/notchedpolyominoes/start.html

Second, even small polyominoes have a lot of perimeter segments, so the number of markings explodes quickly. One workaround: mark pairs of opposite segments. But this gives you a lot of pieces where the marks have the same orientation in both directions, and only six where the mark orientations differ. For a tiling with matched marks, where the pieces make a circuit, this seems to make it too hard to "crumple" the circuit into a nice shape. But a fence problem only needs four turns, so we have enough to get around. This fence surrounds an area of 208. I do not know if this is maximal. My first attempt surrounded an area of 155, and I did a bunch of tweaking to get to my current best attempt.

#TilingTuesday

Some sublime patterns at the State Museum of Applied Arts of Uzbekistan, Tashkent, Uzbekistan

You can explore some of the collections online at https://artmuseum.uz/collection.html

#TilingTuesday #geometry #tiling #MathArt #photography #design #IslamicPattern #IslamicArt

#TilingTuesday #geometry #tiling #MathArt #photography #design #IslamicPattern #IslamicArt

Excerpt of a monohedral 11-gon tiling of a non-compact surface embedded in 𝑅³. (3 11-gons at every vertex)

The surface splits 𝑅³ in two, so that the space within the dodecagonal tunnels is on one side and the space in the hexagonal tunnels on the other.

The labeled dual edges of the tiling form a partial Cayley surface complex of the group:

G = ⟨ f₁, f₂, f₃, t₁, t₂, t₃, t₄ ∣ f₂², t₃², f₁², t₂², f₃², t₄³, t₁³, (t₁t₄)², f₁t₃t₄⁻¹, f₃t₁⁻¹t₂⁻¹, (f₁f₃)², f₂t₂t₃⁻¹⟩

(1/n) #tilingTuesday #math #3d #geometry #genuary

#genuary #genuary2026 Day 17: Wallpaper Group

#tilingtuesday I thought this would be a pain to do but it worked out ok. Still, a lot of effort. I started off using https://tiled.art/ but once I'd made a good enough path I extracted it and switched to #p5js; probably a mistake, the code is horrible

Tilings and tessellations are such an interesting area of mathematics. They seem so simple that everything should have been discovered already, and yet new fundamental questions are raised every year!

In this case, researchers wondered about "soft" tilings, i.e. tilings with as few corners as possible and are entirely "rounded" elsewhere. It turns out they are everywhere in nature, both in 2D and 3D. And you can have tilings of three-dimensional spaces that have no corners at all!

https://www.reviewertoo.com/tessellation-revelation/
#TilingTuesday

So I tried implementing ðe Weierstrass-Mandelbrot function coz I mean it's called ðe Weierstrass-Mandelbrot function I had to check it out 𓅱
apparently it's a lot like my weierstrass-derived aperiodic "tiling" posts but in ðe uncanny valley towards ðe terrain direction in abstract concept space 🤔🤔🤔

#liminal #TilingTuesday #gonewrong #noise #aperiodic #creativecoding #mathart #procgen #abstract