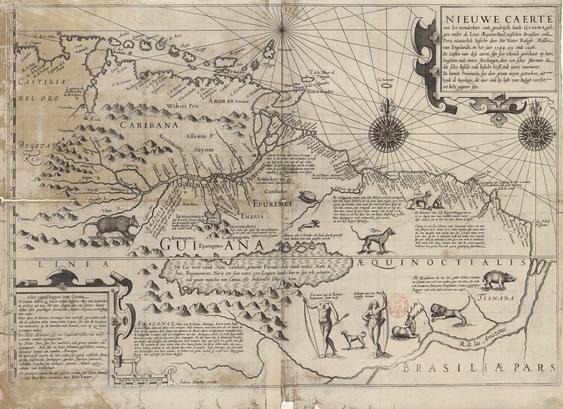
A Scientific American story on the cognitive benefits of hand-annotating books inspired my latest newsletter on maps, monsters, and making sense of Sir Walter Ralegh's "Brief and True History of Guiana" (1596).

#history #histsci #earlymodern #manuscript #maps #cartography

https://buttondown.com/surekhadavies/archive/walter-raleghs-headless-monsters-and-annotation/

For the #spacetober_challenge day 6 prompt constellation, I am sharing my portrait of #astronomer Henrietta Swan Leavitt (1868-1921) who set the scale of our Universe. My portrait of Leavitt is printed in silvery lavender ink on Japanese kozo (or mulberry paper). Behind her is a line showing stellar luminosity (capital L with subscript sun-symbol, a circle with a dot) as a function of time (t). 🧵

#linocut #printmaking #WomenInSTEM #sciart #histsci #astronomy #constellation #mastoArt

I tried to find previous discussion/announcements about the loss of the #OpenAccess Einstein Digital Papers site.

There is this article (which I think reads like a regurgitated press release) from April on ‘The Bookseller’ about the new subscription database that will replace the site: https://web.archive.org/web/20250417124615/https://www.thebookseller.com/news/paradigm-publishing-services-and-princeton-university-press-partner-on-new-einstein-database

Note that it says *nothing* about shutting down the open-access site.

But it informs us that the new database will be ‘the first complete picture of the massive written legacy capturing the full range of Einstein’s work’. (How was the previous site any less complete? Except for the still-to-be-published volumes of papers, which presumably will only be added to the database when they are released.)

And, according to the editorial director at Princeton University Press, the new database ‘will introduce Einstein’s world-changing work to a new generation of researchers’. (A ‘new generation’ comprising only those whose institutions are able and willing to pay for access, or who can afford to pay themselves.)

1/2

#HistSci #Einstein

I have just noticed that the previously-#OpenAccess Digital Einstein Papers site is no longer available, and will become a subscription database [https://einsteinpapers.press.princeton.edu/einstein-database/]. Apparently the site was taken down in mid-August.

I consider this a grievous loss to scholarship. When I was writing my book ‘Form & Number’, I scoured Einstein's papers for anywhere he mentioned mathematical beauty.

As far as I can see, access via the Wayback Machine [https://web.archive.org/web/20250810010714/https://einsteinpapers.press.princeton.edu/] is at best unreliable – many page images are not loading for me.

(Some of the early volumes of the Collected Papers are available on the Internet Archive.)

#HistSci #Einstein

📚 **The Collected Papers Of Albert Einstein**

Volume One: https://archive.org/details/the-collected-papers-of-albert-einstein-vol-l/.

Volume Two: https://archive.org/details/the-collected-papers-of-albert-einstein-vol-2-1900-1909.

Volume Three: https://archive.org/details/the-collected-papers-of-albert-einsten-volume-3-the-swiss-year-1909-1911.

Volume Six: https://archive.org/details/the-collected-papers-of-albert-einstein-vol.-6-the-berlin-years-writings-1914-1917.

#History #Histodons #HistSci #Science #Einstein #Academia

Danish astronomer and Tycho Brahe's chief assistant, Christen Sørensen, aka Longomontanus, was born 4 October 1562 #histsci

https://thonyc.wordpress.com/2018/08/08/tychos-last-bastion/

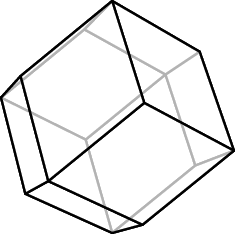
The #Mathober day 3 prompt is ‘#Polyhedron’. I have no art to offer, but I thought I would use the occasion to draw attention to a lesser-known role of polyhedra in Johannes Kepler's (1571–1630) thought.

Start with the famous part: Kepler argued that the five regular (or Platonic) solids fitted between the orbs of the then-known six planets [https://commons.wikimedia.org/wiki/File:Kepler-solar-system-1.png].

When Galileo discovered four moons of Jupiter, Kepler sought a similar polyhedral structure for the Jovian system, and suggested that ‘semiregular’ solids provided the key. ‘Semiregular’ for Kepler meant that the polyhedra had rhombic faces and satisfied certain technical criteria. (The concept differs from today's notion of semiregular polyhedra.)

There were exactly three such ‘semiregular’ polyhedra:

• the cube (the square being a special kind of rhombus).

• the rhombic dodecahedron (12 faces; diagram attached).

• the rhombic triacontahedron (30 faces; diagram attached).

Kepler placed the rhombic dodecahedron between Io and Europa, the rhombic triacontahedron between Europa and Ganymede, and the cube between Ganymede and Callisto.

Kepler thought that there were six planets because God had shaped the cosmos around the five platonic solids. The three ‘semiregular’ solids would similarly explain why there were four moons of Jupiter.

Perhaps someone who is a better artist than I am could draw a diagram of the three rhombic solids and the orbs of the four Galilean moons in the style of Kepler's famous diagram of the Platonic solids between the orbs of the planets.

#Mathober2025 #HistMath #HistSci