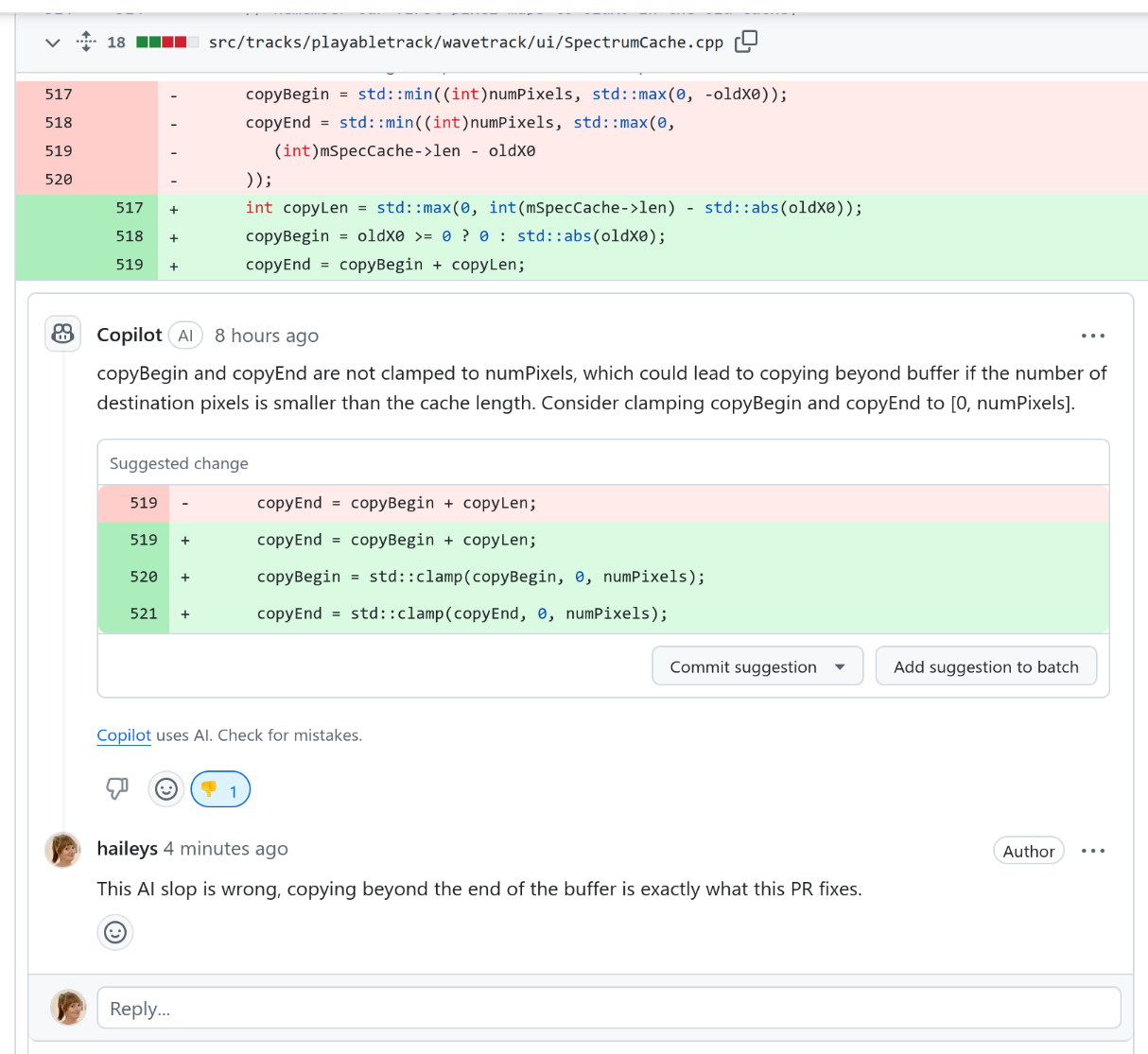
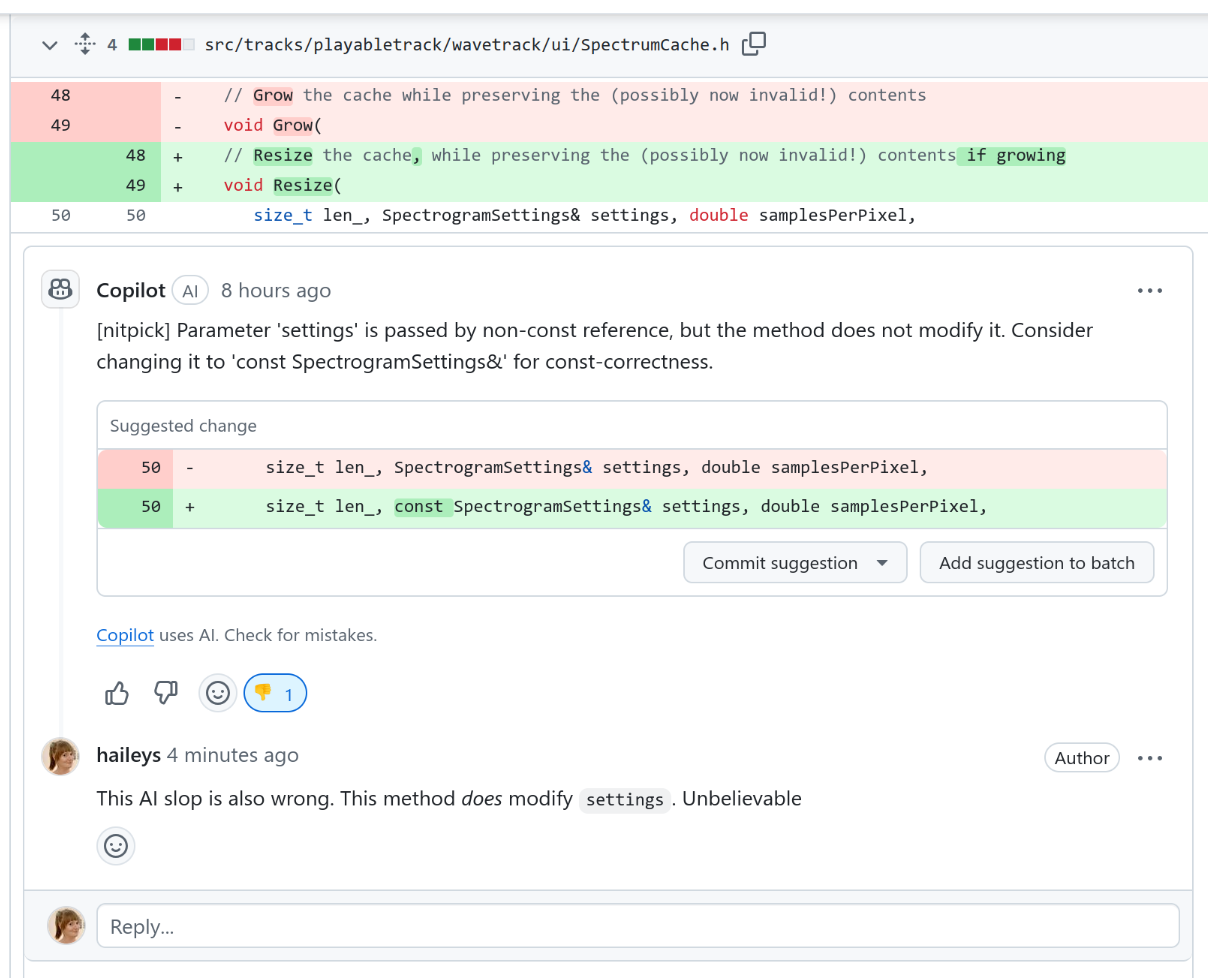
Slice categories and continuations are very similar concepts, with a lot of overlap between the two. Yet I'm somewhat confident that there are differences as well. Anybody have insight?
| Pronouns | he/him |
| Pronouns | he/him |
Slice categories and continuations are very similar concepts, with a lot of overlap between the two. Yet I'm somewhat confident that there are differences as well. Anybody have insight?
Do not take legal advice from chatGPT.
Do not take medical advice from chatGPT.
Do not take financial advice from chatGPT.
In fact, stop using chatGPT. It’s destroying the environment, giving people terrible advice and lining tech bro pockets.
I wish we had spaces to collaborate on technical work where being a jerk was just not allowed. Like, actual proper fearless moderation.
Your reply starts with "No." on its own line? Two weeks ban. Learn to behave.
You go on a tear about another participant? One year ban. No warning.
I'm a privileged white dude with 20k followers and even I hesitate to contribute to some spaces because of the mailing list hand-to-hand combat.
Imagine how many contributions by talented folks we are wasting!
@pigworker Thinking things over a bit this morning, I think I see (sort of) how things are supposed to go.
(Also, adding unification to my map of ideas surrounding the Stern-Brocot tree much too intriguing and important trailhead to pass up... this almost certainly needs to be incorporated into my notes, at least once I understand it better.)
There are clearly details I don't understand, but I was trying to think about pullbacks in the context of the subgroups of Z in the category of groups.
This is... not a great starting point, as all subgroups of Z are isomorphic to each other. But even my imperfect thinking here, I think I can see why unification and gcd could be connected.
And it has, I think, helped rectify some of my past misunderstandings about category theory; traditional abstract algebra often treats isomorphisms very blitheIy, and I think I have been missing something in the "sense and reference" interpretation of what a group "is".
Clearly I need to change my category, and/or particular objects I'm looking at, to arrive at an understanding of a useful result.
@futurebird Three things that come to my mind are purely functional programming, continuations, and continued fractions.
As far as I know, continuations and continued fractions aren't related to each other in any particularly interesting way.
But I've also been toying with the two concepts for decades.
But I've also built my philosophy of math education based around my first "aha" moment with continued fractions.
I'd consider continuations considerably more niche, but it's a very popular niche.
@pigworker Certainly an intriguing trail of breadcrumbs. I tried (and mostly failed) to understand Category Theory as an undergrad. Actually, I've been thinking about exact sequences a bit lately, and they are almost starting to make sense, and as a result category theory is almost starting to make sense as well.
... I don't know how many students need to start looking at exact sequences to start appreciating category theory. That would certainly be well outside the bounds of your class, but I'd love to take it, I'm sure I'd learn a lot!
@pigworker I am very curious about the analogy between unification and gcd in your mind, though, as I personally haven't connected those two concepts.
(I'll admit I almost certainly don't have a particularly deep understanding of unification or why it's interesting... I just tend to resort to it typically as a strategy for solving problems by hand.)