Non-equilibrium dynamics in galaxies that appear to have lots of dark matter: ultrafaint dwarfs
This is a long post. It started focused on ultrafaint dwarfs, but can’t avoid more general issues. In order to diagnose non-equilibrium effects, we have to have some expectation for what equilibrium would be. The Tully-Fisher relation is a useful empirical touchstone for that. How the Tully-Fisher relation comes about is itself theory-dependent. These issues are intertwined, so in addition to discussing the ultrafaints, I also review some of the many predictions for Tully-Fisher, and how our theoretical expectation for it has evolved (or not) over time.
In the last post, we discussed how non-equilibrium dynamics might make a galaxy look like it had less dark matter than similar galaxies. That pendulum swings both ways: sometimes non-equilibrium effects might stir up the velocity dispersion above what it would nominally be. Some galaxies where this might be relevant are the so-called ultrafaint dwarfs (not to be confused with ultradiffuse galaxies, which are themselves often dwarfs). I’ve talked about these before, but more keep being discovered, so an update seems timely.
Galaxies and ultrafaint dwarfs
It’s a big universe, so there’s a lot of awkward terminology, and the definition of an ultrafaint dwarf is somewhat debatable. Most often I see them defined as having an absolute magnitude limit MV > -8, which corresponds to a luminosity less than 100,000 suns. I’ve also seen attempts at something more physical, like being a “fossil” whose star formation was entirely before cosmic reionization, which ended way back at z ~ 6 so all the stars would be at least*&^# 12.5 Gyr old. While such physics-based definitions are appealing, these are often tied up with theoretical projection: the UV photons that reionized the universe should have evaporated the gas in small dark matter halos, so these tiny galaxies can only be fossils from before that time. This thinking pervades much of the literature despite it being obviously wrong, as counterexamples! exist. For example, Leo P is practically an ultrafaint dwarf by luminosity, but has ample gas (so a larger baryonic mass) and is currently forming stars.
A luminosity-based definition is good enough for us here; I don’t really care exactly where we make the cut. Note that ultrafaint is an appropriate moniker: a luminosity of 105 L☉ is tiny by galaxy standards. This is a low-grade globular cluster, and some ultrafaints are only a few hundred solar luminosities, which is barely even# a star cluster. At this level, one has to worry about stochastic effects in stellar evolution. If there are only a handful of stars, the luminosity of the entire system changes markedly as a single star evolves up the red giant branch. Consequently, our mapping from observed quantities to stellar mass is extremely dodgy. For consistency, to compare with brighter dwarfs, I’ve adopted the same boilerplate M*/LV = 2 M☉/L☉. That makes for a fair comparison luminosity-to-luminosity, but the uncertainty in the actual stellar mass is ginormous.
It gets worse, as the ultrafaints that we know about so far are all very nearby satellites of the Milky Way. They are not discovered in the same way as other galaxies, where one plainly sees a galaxy on survey plates. For example, NGC 7757:
The spiral galaxy NGC 7757 as seen on plates of the Palomar Sky Survey.While bright, high surface brightness galaxies like NGC 7757 are easy to see, lower surface brightness galaxies are not. However, they can usually still be seen, if you know where to look:
UGC 1230 as seen on the Palomar Sky Survey. It’s in the middle.I like to use this pair as an illustration, as they’re about the same distance from us and about the same angular size on the sky – at least, once you crank up the gain for the low surface brightness UGC 1230:
Zoom in on deep CCD images of NGC 7757 (left) and UGC 1230 (right) with the contrast of the latter enhanced. The chief difference between the two is surface brightness – how spread out their stars are. They have a comparable physical diameter, they both have star forming regions that appear as knots in their spiral arms, etc. These galaxies are clearly distinct from the emptiness of the cosmic void around them, being examples of giant stellar systems that gave rise to the term “island universe.”In contrast to objects that are obvious on the sky as independent island universes, ultrafaint dwarfs are often invisible to the eye. They are recognized as a subset of stars near each other on the sky that also share the same distance and direction of motion in a field that might otherwise be crowded with miscellaneous, unrelated stars. For example, here is Leo IV:
The ultrafaint dwarf Leo IV as identified by the Sloan Digital Sky Survey and the Hubble Space Telescope.See it?
I don’t. I do see a number of background galaxies, including an edge-on spiral near the center of the square. Those are not the ultrafaint dwarf, which is some subset of the stars in this image. To decide which ones are potentially a part of such a dwarf, one examines the color magnitude diagram of all the stars to identify those that are consistent with being at the same distance, and assigns membership in a probabilistic way. It helps if one can also obtain radial velocities and/or proper motions for the stars to see which hang together – more or less – in phase space.
Part of the trick here is deciding what counts as hanging together. A strong argument in favor of these things residing in dark matter halos is that the velocity differences between the apparently-associated stars are too great for them to remain together for any length of time otherwise. This is essentially the same situation that confronted Zwicky in his observations of galaxies in clusters in the 1930s. Here are these objects that appear together in the sky, but they should fly apart unless bound together by some additional, unseen force. But perhaps some of these ultrafaints are not hanging together; they may be in the process of coming apart. Indeed, they may have so few stars because they are well down the path of dissolution.
Since one cannot see an ultrafaint dwarf in the same way as an island universe, I’ve heard people suggest that being bound by a dark matter halo be included in the definition of a galaxy. I see where they’re coming from, but find it unworkable. I know a galaxy when I see one. As did Hubble, as did thousands of other observers since, as can you when you look at the pictures above. It is absurd to make the definition of an object that is readily identifiable by visual inspection be contingent on the inferred presence of invisible stuff.
So are ultrafaints even galaxies? Yes and no. Some of the probabilistic identifications may be mere coincidences, not real objects. However, they can’t all be fakes, and I think that if you put them in the middle of intergalactic space, we would recognize them as galaxies – provided we could detect them at all. At present we can’t, but hopefully that situation will improve with the Rubin Observatory. In the meantime, what we have to work with are these fragmentary systems deep in the potential well of the seventy billion solar mass cosmic gorilla that is the Milky Way. We have to be cognizant that they might have gotten knocked around, as we can see in more massive systems like the Sagittarius dwarf. Of course, if they’ve gotten knocked around too much, then they shouldn’t be there at all. So how do these systems evolve under the influence of a comic gorilla?
Let’s start by looking at the size-mass diagram, as we did before. Ultrafaint dwarfs extend this relation to much lower mass, and also to rather small sizes – some approaching those of star clusters. They approximately follow a line of constant surface density, ~0.1 M☉ pc-2 (dotted line)..
The size and stellar mass of Local Group dwarfs as discussed previously, with the addition of ultrafaint dwarfs$ (small gray squares).This looks weird to me. All other types of galaxies scatter all over the place in this diagram. The ultrafaints are unique in following a tight line in the size-mass plane, and one that follows a line of constant surface brightness. Every element of my observational experience screams that this is likely to be an artifact. Given how these “galaxies” are identified as the loose association of a handful of stars, it is easy to imagine that this trend might be an artifact of how we define the characteristic size of a system that is essentially invisible. It might also arise for physical reasons to do with the cosmic gorilla; i.e., it is a consequence of dynamical evolution. So maybe this correlation is real, but the warning lights that it is not are flashing red.
The Baryonic Tully-Fisher relation as a baseline
Ideally, we would measure accelerations to test theories, particularly MOND. Here, we would need to use the size to estimate the acceleration, but I straight up don’t believe these sizes are physically meaningful. The stellar mass, dodgy as it is, seems robust by comparison. So we’ll proceed as if we know that much – which we don’t, really – but let’s at least try.
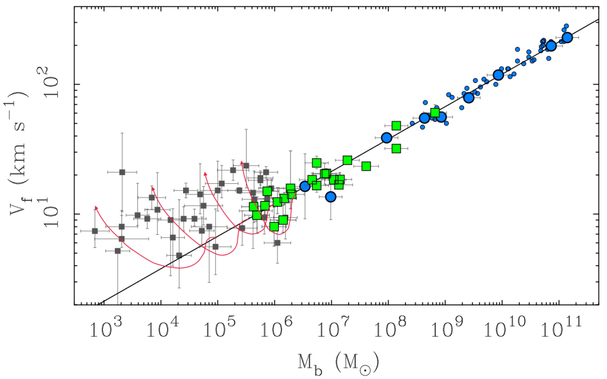
With the stellar mass (there is no gas in these things), we are halfway to constructing the baryonic Tully-Fisher relation (BTFR), which is the simplest test of the dynamics that we can make with the available data. The other quantity we need is the characteristic circular speed of the gravitational potential. For rotating galaxies, that is the flat rotation speed, Vf. For pressure supported dwarfs, what is usually measured is the velocity dispersion σ. We’ve previously established that for brighter dwarfs in the Local Group, a decent approximation is Vf = 2σ, so we’ll start by assuming that this should apply to the ultrafaints as well. This allows us to plot the BTFR:
The baryonic mass and characteristic circular speeds of both rotationally supported galaxies (circles) and pressure supported dwarfs (squares). The colored points follow the same baryonic Tully-Fisher relation (BTFR), but the data for low mass ultrafaint dwarfs (gray squares) flattens out, having nearly the same characteristic speed over several decades in mass.The BTFR is an emprical relation of the form Vf ~ Mb1/4 over about six decades in mass. Somewhere around the ultrafaint scale, this no longer appears to hold, with the observed velocity flattening out to become approximately constant for these lowest mass galaxies. I’m not sure this is real, as there many practical caveats to interpreting the observations. Measuring stellar velocities is straightforward but demanding at this level of accuracy. There are many potential systematics, pretty much all of which cause the intrinsic velocity dispersion to be overestimated. For example, observations made with multislit masks tend to return larger dispersions than observations of the same object with fibers. That’s likely because it is hard to build a mask so well that all of the stars perfectly hit the centers of the slitlets assigned to them; offsets within the slit shift the spectrum in a way that artificially adds to the apparent velocity dispersion. Fibers are less efficient in their throughput, but have the virtue of blending the input light in a way that precludes this particular systematic. Another concern is physical – some of the stars that are observed are presumably binaries, and some of the velocity will be due to motion within the binary pair and nothing to do with the gravitational potential of the larger system. This can be addressed with repeated observations to see if some velocities change, but it is hard to do that for each and every system, especially when it is way more fun to discover and explore new systems than follow up on the same one over and over and over again.
There are lots of other things that can go wrong. At some level, some of them probably do – that’s the nature of observational astronomy&. While it seems likely that some of the velocity dispersions are systematically overestimated, it seems unlikely that all of them are. Let’s proceed as if the bulk of the data is telling us something, even if we treat individual objects with suspicion.
MOND
MOND makes a clear prediction for the BTFR of isolated galaxies: the baryonic mass goes as the fourth power of the flat rotation speed. Contrary to Newtonian expectation, this holds irrespective of surface brightness, which is what attracted my attention to the theory in the first place. So how does it do here?
The same data as above with the addition of the line predicted by MOND (Milgrom 1983).Low surface density means low acceleration, so low surface brightness galaxies would make great tests of MOND if they were isolated. Oh, right – they already did. Repeatedly. MOND also correctly predicted the velocities of low mass, gas-rich dwarfs that were unknown when the prediction was made. These are highly nontrivial successes of the theory.
The ultrafaints we’re discussing here are not isolated, so they do not provide the clean tests that isolated galaxies provide. However, galaxies subject to external fields should have low velocities relative to the BTFR, while the ultrafaints have higher velocities. They’re on the wrong side of the relation! Taking this at face value (i.e., assuming equilibrium), MOND fails here.
Whenever MOND has a problem, it is widely seen as a success of dark matter. In my experience, this is rarely true: observations that are problematic for MOND usually don’t make sense in terms of dark matter either. For each observational test we also have to check how LCDM fares.
LCDM
How LCDM fares is often hard to judge because its predictions for the same phenomena are not always clear. Different people predict different things for the same theory. There have been lots of LCDM-based predictions made for both dwarf satellite galaxies and the Tully-Fisher relation. Too many, in fact – it is a practical impossibility to examine them all. Nevertheless, some common themes emerge if we look at enough examples.
The halo mass-velocity relation
The most basic prediction of LCDM is that the mass of a dark matter halo scales with the cube of the circular velocity of a test particle at the virial radius (conventionally taken to be the radius R200 that encompasses an average density 200 times the critical density of the universe. If that sounds like gobbledygook to you, just read “halo” for “200”): M200 ~ V2003. This is a very basic prediction that everyone seems to agree to.
There is a tiny problem with testing this prediction: it refers to the dark matter halo that we cannot see. In order to test it, we have to introduce some scaling factors to relate the dark to the light. Specifically, Mb = fd M200 and Vf = fv V200, where fd is the observed fraction of mass in baryons and fv relates the observed flat velocity to the circular speed of our notional test particle at the virial radius. The obvious assumptions to make are that fd is a constant (perhaps as much as but not more than the cosmic baryon fraction of 16%) and fv is close to untiy. The latter requirement stems from the need for dark matter to explain the amplitude of the flat rotation speed, but fv could be slightly different; plausible values range from 0.9 < fv < 1.4. Values large than one indicate a rotation curve that declines before the virial radius is reached, which is the natural expectation for NFW halos.
Here is a worked example with fd = 0.025 and fv = 1:
The same data as above with the addition of the nominal prediction of LCDM. The dotted line is the halo mass-circular velocity relation; the gray band is a simple model with fd = 0.025 and fv = 1 (e.g., Mo, Mao, & White 1998).I have illustrated the model with a fat grey line because fd = 0.025 is an arbitrary choice* I made to match the data. It could be more, it could be less. The detected baryon fraction can be anythings up to or less than the cosmic value, fd < fb = 0.16 as not all of the baryons available in a halo cool and condense into cold gas that forms visible stars. That’s fine; there’s no requirement that all of the baryons have to become readily observable, but there is also no reason to expect all halos to cool exactly the same fraction of baryons. Naively one would expect at least some variation in fd from halo to halo, so there could and probably should be a lot of scatter: the gray line could easily be a much wider band than depicted.
In addition to the rather arbitrary value of fd, this reasoning also predicts a Tully-Fisher relation with the wrong slope. Picking a favorable value of fd only matches the data over a narrow range of mass. It was nevertheless embraced for many years by many people. Selection effects bias samples to bright galaxies. Consequently, the literature is rife with TF samples dominated by galaxies with Mb > 1010 M☉ (the top right corner of the plot above); with so little dynamic range, a slope of 3 looks fine. Once you look outside that tiny box, it does not look fine.
Personally, I think a slope of 3 is an oversimplification. That is the prediction for dark matter halos; there can be effects that vary systematically with mass. An obvious one is adiabatic compression, the effect by which baryons drag some dark matter along with them as they settle to the center of their halos. This increases fv by an amount that depends on the baryonic surface density. Surface density correlates with mass, so I would nominally expect higher velocities in brighter galaxies; this drives up the slope. There are various estimates of this effect; typically one gets a slope like 3.3, not the observed 4. Worse, it predicts an additional effect: at a given mass, galaxies of higher surface brightness should also have higher velocity. Surface brightness should be a second parameter in the Tully-Fisher relation, but this is not observed.
The easiest way to reconcile the predicted and observed slopes are to make fd a function of mass. Since Mb = fd M200 and M200 ~ V2003, Mb ~ fd V2003. Adopting fv = 1 for simplicity, Mb ~ Vf4 follows if fd ~ Vf. Problem solved, QED.
There are [at least] two problems with this argument. One is that the scaling fd ~ Vf must hold perfectly without introducing any scatter. This is a fine-tuning problem: we need one parameter to vary precisely with an another, unrelated parameter. There is no good reason to expect this; we just have to insert the required dependence by hand. This is much worse than choosing an arbitrary value for fd: now we’re making it a rolling fudge factor to match whatever we need it to. We can make it even more complicated by invoking some additional variation in fv, but this just makes the fine-tuning worse as the product fdfv-3 has to vary just so. Another problem is that what we’re doing all this to adjust the prediction of one theory (LCDM) to match that of a different theory (MOND). It is never a good sign when we have to do that, whether we admit it or not.
Abundance matching
The reasoning leading to a slope 3 Tully-Fisher relation assumes a one-to-one relation between baryonic and halo mass (fd = constant). This is an eminently reasonable assumption. We spent a couple of decades trying to avoid having to break this assumption. Once we do so and make fd a freely variable parameter, then it can become a rolling fudge factor that can be adjusted to fit anything. Everyone agrees that is Bad. However, it might be tolerable if there is an independent way of estimating this variation. Rather than make fd just be what we need it to be as described above, we can instead estimate it with abundance matching.
Abundance matching comes from equating the observed number density of galaxies as a function of mass with the number density of dark matter halos. This process gives fd, or at least the stellar fraction, f*, which is close to fd for bright galaxies. Critically, it provides a way to assign dark matter halo masses to galaxies independently of their kinematics. This replaces an arbitrary, rolling fudge factor with a predictive theory.
Abundance matching models generically introduce curvature into the prediction for the BTFR. This stems from the mismatch in the shape of the galaxy stellar mass function (a Schechter function) and the dark halo mass function (a power law on galaxy scales). This leads to a bend in relations that map between visible and dark mass.
The transition from the M ~ V3 reasoning to abundance matching occurred gradually, but became pronounced circa 2010. There are many abundance matching models; I already faced the problem of the multiplicity of LCDM predictions when I wrote a lengthy article on the BTFR in 2012. To get specific, let’s start with an example from then, the model of Trujillo-Gomez-et al. (2011):
The same data as above with the addition of the line predicted by LCDM in the model of Trujillo-Gomez-et al. (2011).One thing Trujillo-Gomez-et al. (2011) say in their abstract is “The data present a clear monotonic LV relation from ∼50 km s−1 to ∼500 km s−1, with a bend below ∼80 km s−1“. By LV they mean luminosity-velocity, i.e., the regular Tully-Fisher relation. The bend they note is real; that’s what happens when you consider only the starlight and ignore the gas. The bend goes away if you include that gas. This was already known at the time – our original BTFR paper from 2000 has nearly a thousand citations, so it isn’t exactly obscure. Ignoring the gas is a choice that makes no sense empirically but makes a lot of sense from the perspective of LCDM simulations. By 2010, these had become reasonably good at matching the numbers of stars observed in galaxies, but the gas properties of simulated galaxies remained, hmmmmmmm, wanting. It makes sense to utilize the part that works. It makes less sense to pretend that this bend is something physically meaningful rather than an artifact of ignoring the gas. The pressure-supported dwarfs are all star dominated, so this distinction doesn’t matter here, and they follow the BTFR, not the stars-only version.
An old problem in galaxy formation theory is how to calibrate the number density of dark matter halos to that of observed galaxies. For a long time, a choice that people made was to match either the luminosity function or the kinematics. These didn’t really match up, so there was occasional discussion of the virtues and vices of the “luminosity function calibration” vs. the “Tully-Fisher calibration.” These differed by a factor of ~2. This tension between remains with us. Mostly simulations have opted to adopt the luminosity function calibration, updated and rebranded as abundance matching. Again, this makes sense from the perspective of LCDM simulations, because the number density of dark matter halos is something that simulations can readily quantify while the kinematics of individual galaxies are much harder to resolve**.
The nonlinear relation between stellar mass and halo mass obtained from abundance matching inevitably introduces curvature into the corresponding Tully-Fisher relation predicted by such models. That’s what you see in the curved line of Trujillo-Gomez-et al. (2011) above. They weren’t the first to obtain such a result, and the certainly weren’t the last: this is a feature of LCDM with abundance matching, not a bug.
The line of Trujillo-Gomez-et al. (2011) matches the data pretty well at intermediate masses. It diverges to higher velocities at both small and large galaxy masses. I’ve written about this tension at high masses before; it appears to be real, but let’s concentrate on low masses here. At low masses, the velocity of galaxies with Mb < 108 M☉ appears to be overestimated. But the divergence between model and reality has just begun, and it is hard to resolve small things in simulations, so this doesn’t seem too bad. Yet.
Moving ahead, there are the “Latte” simulations of Wetzel et al. (2016) that use the well-regarded FIRE code to look specifically at simulated dwarfs, both isolated and satellites – specifically satellites of Milky Way-like systems. (Milky Way. Latte. Get it? Nerd humor.) So what does that find?
The same data as above with the addition of simulated dwarfs (orange triangles) from the Latte LCDM simulation of Wetzel et al. (2016), specifically the simulated satellites in the top panel of their Fig. 3. Note that we plot Vf = 2σ for pressure supported systems, both real and simulated.The individual simulated dwarf satellites of Wetzel et al. (2016) follow the extrapolation of the line predicted by Trujillo-Gomez-et al. (2011). To first order, it is the same result to higher resolution (i.e., smaller galaxy mass). Most of the simulated objects have velocity dispersions that are higher than observed in real galaxies. Intriguingly, there are a couple of simulated objects with M* ~ 5 x 106 M☉ that fall nicely among the data where there are both star-dominated and gas-rich galaxies. However, these two are exceptions; the rule appears to be characteristic speeds that are higher than observed.
The lowest mass simulated satellite objects begin to approach the ultrafaint regime, but resolution continues to be an issue: they’re not really there yet. This hasn’t precluded many people from assuming that dark matter will work where MOND fails, which seems like a heck of a presumption given that MOND has been consistently more successful up until that point. Where MOND underpredicts the characteristic velocity of ultrafaints, LCDM hasn’t yet made a clear prediction, and it overpredicts velocities for objects of slightly larger mass. Ain’t no theory covering itself in glory here, but this is a good example where objects that are a problem for MOND are also a problem for dark matter, and it seems likely that non-equilibrium dynamics play a role in either case.
Comparing apples with apples
A persistent issue with comparing simulations to reality is extracting comparable measures. Where circular velocities are measured from velocity fields in rotating galaxies and estimated from measured velocity dispersions in pressure supported galaxies, the most common approach to deriving rotation curves from simulated objects is to sum up particles in spherical shells and assume V2 = GM/R. These are not the same quantities. They should be proxies for one another, but equality holds only in the limit of isotropic orbits in spherical symmetry. Reality is messier than that, and simulations aren’t that simple either%.
Sales et al. (2017) make the effort to make a better comparison between what is observed given how it is observed, and what the simulations would show for that quantity. Others have made a similar effort; a common finding is that the apparent rotation speeds of simulated gas disks do not trace the gravitational potential as simply as GM/R. That’s no surprise, but most simulated rotation curves do not look like those of real galaxies^, so the comparison is not straightforward. Those caveats aside, Sales et al. (2017) are doing the right thing in trying to make an apples-to-apples comparison between simulated and observed quantities. They extract from simulations a quantity Vout that is appropriate for comparison with what we observe in the outer parts of rotation curves. So here is the resulting prediction for the BTFR:
The same data as above with the addition of the line predicted by LCDM in the model of Sales et al. (2017), specifically the formula for Vout in their Table 2 which is their proxy for the observable rotation speed.That’s pretty good. It still misses at high masses (those two big blue points at the top are Andromeda and the Milky Way) and it still bends away from the data at low masses where there are both star-dominated and gas-rich galaxies. (There are a lot more examples of the latter that I haven’t used here because the plot gets overcrowded.) Despite the overshoot, the use of an observable aspect of the simulations gets closer to the data, and the prediction flattens out in the same qualitative sense. That’s good, so one might see cause for hope that this problem is simply a matter of making a fair comparison between simulations and data. We should also be careful not to over-interpret it: I’ve simply plotted the formula they give; the simulations to which they fit it surely do not resolve ultrafaint dwarfs, so really the line should stop at some appropriate mass scale.
Nevertheless, it makes sense to look more closely at what is observed vs. what is simulated. This has recently been done in greater detail by Ruan et al. (2025). They consider two simulations that implement rather different feedback; both wind up producing rotating, gas rich dwarfs that actually fall on the BTFR.
The same data as above with the addition of simulated dwarfs of Ruan et al. (2025), specifically from the top right panel of their Fig. 6. The orange circles are their “massives” and the red triangles the “marvels” (the distinction refers to different feedback models).Finally some success after all these years! Looking at this, it is tempting to declare victory: problem solved. It was just a matter of doing the right simulation all along, and making an apples-to-apples comparison with the data.
That sounds too goo to be true. Is it repeatable in other simulations? What works now that didn’t before?
These are high resolution simulations, but they still don’t resolve ultrafaints. We’re talking here about gas-rich dwarfs. That’s also an important topic, so let’s look more closely. What works now is in the apples-to-apples assessment: what we would measure for Vout is less than Vmax (related to V200) of the halo:
Two panels from Fig. 7 of Ruan et al. (2025) showing the ratio of the velocity we might observe relative to the characteristic circular velocity of the halo (top) and the ratio of the radii where these occur (bottom).The treatment of cold gas in simulations has improved. In these simulations, Vout(Rout) is measured where the gas surface density falls to 1 M☉ pc-2, which is typical of many observations. But the true rotation curve is still rising for objects with Mb < a few x 108 M☉; it has not yet reached a value that is characteristic of the halo. So the apparent velocity is low, even if the dark matter halos are doing basically the same thing as before:
As above, but with the addition of the true Vmax (small black dots) of the simulated halos discussed by Ruan et al. (2025), which follow the relation of Sales et al. (2017) (line for Vmax in their Table 2).I have mixed feelings about this. On the one hand, there are many dwarf galaxies with rising rotation curves that we don’t see flatten out, so it is easy to imagine they might keep going up, and I find it plausible that this is what we would find if we looked harder. So plausible that I’ve spend a fair amount of time doing exactly this. Not all observations terminate at 1 M☉ pc-2, and whenever we push further out, we see the same damn thing over and over: the rotation curve flattens out and stays flat!!. That’s been my anecdotal experience; getting beyond that systematically is the point of the MOHNGOOSE survey. This was constructed to detect much lower atomic gas surface densities, and routinely detects gas at the 0.1 M☉ pc-2 level where Ruan et al. suggest we should see something closer to Vmax. So far, we don’t.
I don’t want to sound too negative, because how we map what we predict in simulations to what we measure in observations is a serious issue. But it seems a bit of a stretch for a low-scatter power law BTFR to be the happenstance of observational sensitivity that cuts in at a convenient mass scale. So far, we see no indication of that in more sensitive observations. I’ll certainly let you know if that changes.
Survey says…
At this juncture, we’ve examined enough examples that the reader can appreciate my concern that LCDM models can predict rather different things. What does the theory really predict? We can’t really test it until we agree what it should do!!!.
I thought it might be instructive to combine some of the models discussed above. It is.
Some of the LCDM predictions discussed above shown together. The dotted line to the right of the data is the halo mass-velocity relation, which is the one thing we all agree LCDM predicts but which is observationally inaccessible. The grey band is a Mo, Mao, & White-type model with fd = 0.025. The red dotted line is the model of Trujillo-Gomez-et al. (2011); the solid red line that of Sales et al. (2017) for Vmax.The models run together, more or less, for high mass galaxies. Thanks to observational selection effects, these are the objects we’ve always known about and matched our theories to. In order to test a theory, one wants to force it to make predictions in new regimes it wasn’t built for. Low mass galaxies do that, as do low surface brightness galaxies, which are often but not always low mass. MOND has done well for both, down to the ultrafaints we’re discussing here. LCDM does not yet explain those, or really any of the intermediate mass dwarfs.
What really disturbs me about LCDM models is their flexibility. It’s not just that they miss, it’s that it is possible to miss the data on either side of the BTFR. The older fd = constant models predict velocities that are too low for low mass galaxies. The more recent abundance matching models predict velocities that are too high for low mass galaxies. I have no doubt that a model can be constructed that gets it right, because there is obviously enough flexibility to do pretty much anything. Adding new parameters until we get it right is an example of epicyclic thinking, as I’ve been pointing out for thirty years. I don’t know what could be worse for an idea like dark matter that is not falsifiable.
We still haven’t come anywhere close to explaining the ultrafaints in either theory. In LCDM, we don’t even know if we should draw a curved line that catches them as if they’re in equilibrium, or start from a power-law BTFR and look for departures from that due to tidal effects. Both are possible in LCDM, both are plausible, as is some combination of both. I expect theorists will pick an option and argue about it indefinitely.
Tidal effects
The typical velocity dispersion of the ultrafaint dwarfs is too high for them to be in equilibrium in MOND. But there’s also pretty much no way these tiny things could be in equilibrium, being in the rough neighborhood dominated by our home, the cosmic gorilla. That by itself doesn’t make an explanation; we need to work out what happens to such things as they evolve dynamically under the influence of a pronounced external field. To my knowledge, this hasn’t been addressed in detail in MOND any more than in LCDM, though Brada & Milgrom addressed some of the relevant issues.
There is a difference in approach required for the two theories. In LCDM, we need to increase the resolution of simulations to see what happens to the tiniest of dark matter halos and their resident galaxies within the larger dark matter halos of giant galaxies. In MOND we have to simulate the evolution along the orbit of each unique individual. This is challenging on multiple levels, as each possible realization of a MOND theory requires its own code. Writing a simulation code for AQUAL requires a different numerical approach than QUMOND, and those are both modifications of gravity via the Poisson euqation. We don’t know which might be closer to reality; heck, we don’t even know [yet] if MOND is a modification of gravity or intertia, the latter being even harder to code.
Cold dark matter is scale-free, so crudely I expect ultrafaint dwarfs in LCDM to do the same as larger dwarf satellites that have been simulated: their outer dark matter halos are gradually whittled away by tidal stripping for many Gyr. At first the stars are unaffected, but eventually so little dark matter is left that the stars start to be lost impulsively during pericenter passages. Though the dark matter is scale free, the stars and the baryonic physics that made them are not, so that’s where it gets tricky. The apparent dark-to-luminous mass ratio is huge, so one possibility is that the ultrafaints are in equilibrium despite their environment; they just made ridiculously few stars from the amount of mass available. That’s consistent with a wild extrapolation of abundance matching models, but how it comes about physically is less clear. For example, at some low mass, a galaxy would make so few stars that none are massive enough to result in a supernova, so there is no feedback, which is what is preventing too many stars from forming. Awkward. Alternately, the constant exposure to tidal perturbation might stir things up, with the velocity dispersion growing and stars getting stripped to form tidal streams, so they may have started as more massive objects. Or some combination of both, plus the evergreen possibility of things that don’t occur to me offhand.
Equilibrium for ultrafaint satellites is not an option in MOND, but tidal stirring and stripping is. As a thought experiment, let’s imagine what happens to a low mass dwarf typical of the field that falls towards the Milky Way from some large distance. Initially gas-rich, the first environmental effect that it is likely to experience is ram pressure stripping by the hot coronal gas around the Milky Way. That’s a baryonic effect that happens in either theory; it’s nothing to do with the effective law of gravity. A galaxy thus deprived of much of its mass will be out of equilibrium; its internal velocities will be typical of the original mass but the stripped mass is less. Consequently, its structure must adjust to compensate; perhaps dwarf Irregulars puff up and are transformed into dwarf Spheroidals in this way. Our notional infalling dwarf may have time to equilibrate to its new mass before being subject to strong tidal perturbation by the Milky Way, or it may not. If not, it will have characteristic internal velocities that are too high for its new mass, and reside above the BTFR. I doubt this suffices to explain [m]any of the ultrafaints, as their masses are so tiny that some stellar mass loss is also likely to have occurred.
Let’s suppose that our infalling dwarf has time to [approximately] equilibrate, or it simply formed nearby to begin with. Now it is a pressure supported system [more or less] on the BTFR. As it orbits the Milky Way, it feels an extra force from the external field. If it stays far enough out to remain in quasi-equilibrium in the EFE regime, then it will oscillate in size and velocity dispersion in phase with the strength of the external field it feels along its orbit.
If instead a satellite dips too close, it will be tidally disturbed and depart from equilibrium. The extra energy may stir it up, increasing its velocity dispersion. It doesn’t have the mass to sustain that, so stars will start to leak out. Tidal disruption will eventually happen, with the details depending on the initial mass and structure of the dwarf and on the eccentricity of its orbit, the distance of closest approach (pericenter), whether the orbit is prograde or retrograde relative to any angular momentum the dwarf may have… it’s complicated, so it is hard to generalize##. Nevertheless, we (McGaugh & Wolf 2010) anticipated that “the deviant dwarfs [ultrafaints] should show evidence of tidal disruption while the dwarfs that adhere to the BTFR should not.” Unlike LCDM where most of the damage is done at closest approach, we anticipate for MOND that “stripping of the deviant dwarfs should be ongoing and not restricted to pericenter passage” because tides are stronger and there is no cocoon of dark matter to shelter the stars. The effect is still maximized at pericenter, its just not as impulsive as in the some of the dark matter simulations I’ve seen.
This means that there should be streams of stars all over the sky. As indeed there are. For example:
Stellar streams in the Milky Way identified using Gaia (Malhan et al. 2018).As a tidally influence dwarf dissolves, the stars will leak out and form a trail. This happens in LCDM too, but there are differences in the rate, coherence, and symmetry of the resulting streams. Perhaps ultrafaint dwarfs are just the last dregs of the tidal disruption process. From this perspective, it hardly matters if they originated as external satellites or are internal star clusters: globular clusters native to the Milky Way should undergo a similar evolution.
Evolutionary tracks
Perhaps some of the ultrafaint dwarfs are the nuggets of disturbed systems that have suffered mass loss through tidal stripping. That may be the case in either LCDM or MOND, and has appealing aspects in either case – we went through all the possibilities in McGaugh & Wolf (2010). In MOND, the BTFR provides a reference point for what a stable system in equilibrium should do. That’s the starting point for the evolutionary tracks suggested here:
BTFR with conceptual evolutionary tracks (red lines) for tidally-stirred ultrafaint dwarfs.Objects start in equilibrium on the BTFR. As they become subject to the external field, their velocity dispersions first decreases as they transition through the quasi-Newtonian regime. As tides kick in, stars are lost and stretched along the satellite’s orbit, so mass is lost but the apparent velocity dispersion increases as stars gradually separate and stretch out along a stream. Their relative velocities no longer represent a measure of the internal gravitational potential; rather than a cohesive dwarf satellite they’re more an association of stars in similar orbits around the Milky Way.
This is crudely what I imagine might be happening in some of the ultrafaint dwarfs that reside above the BTFR. Reality can be more complicated, and probably is. For example, objects that are not yet disrupted may oscillate around and below the BTFR before becoming completely unglued. Moreover, some individual ultrafaints probably are not real, while the data for others may suffer from systematic uncertainties. There’s a lot to sort out, and we’ve reached the point where the possibility of non-equilibrium effects cannot be ignored.
As a test of theories, the better course remains to look for new galaxies free from environmental perturbation. Ultrafaint dwarfs in the field, far from cosmic gorillas like the Milky Way, would be ideal. Hopefully many will be discovered in current and future surveys.
!Other examples exist and continue to be discovered. More pertinent to my thinking is that the mass threshold at which reionization is supposed to suppress star formation has been a constantly moving goal post. To give an amusing anecdote, while I was junior faculty at the University of Maryland (so at least twenty years ago), Colin Norman called me up out of the blue. Colin is an expert on star formation, and had a burning question he thought I could answer. “Stacy,” he says as soon as I pick up, “what is the lowest mass star forming galaxy?” Uh, Hi, Colin. Off the cuff and totally unprepared for this inquiry, I said “um, a stellar mass of a few times 107 solar masses.” Colin’s immediate response was to laugh long and loud, as if I had made the best nerd joke ever. When he regained his composure, he said “We know that can’t be true as reionization will prevent star formation in potential wells that small.” So, after this abrupt conversation, I did some fact-checking, and indeed, the number I had pulled out of my arse on the spot was basically correct, at that time. I also looked up the predictions, and of course Colin knew his business too; galaxies that small shouldn’t exist. Yet they do, and now the minimum known is two orders of magnitude lower in mass, with still no indication that a lower limit has been reached. So far, the threshold of our knowledge has been imposed by observational selection effects (low luminosity galaxies are hard to see), not by any discernible physics.
More recently, McQuinn et al. (2024) have made a study of the star formation histories of Leo P and a few similar galaxies that are near enough to see individual stars so as to work out the star formation rate over the course of cosmic history. They argue that there seems to be a pause in star formation after reionization, so a more nuanced version of the hypothesis may be that reionization did suppress star forming activity for a while, but these tiny objects were subsequently able to re-accrete cold gas and get started again. I find that appealing as a less simplistic thing that might have happened in the real universe, and not just a simple on/off switch that leaves only a fossil. However, it isn’t immediately clear to me that this more nuanced hypothesis should happen in LCDM. Once those baryons have evaporated, they’re gone, and it is far from obvious that they’ll ever come back to the weak gravity of such a small dark matter halo. It is also not clear to me that this interpretation, appealing as it is, is unique: the reconstructed star formation histories also look consistent with stochastic star formation, with fluctuations in the star formation rate being a matter of happenstance that have nothing to do with the epoch of reionization.
#So how are ultrafaint dwarfs different from star clusters? Great question! Wish we had a great answer.
Some ultrafaints probably are star clusters rather than independent satellite galaxies. How do we tell the difference? Chiefly, the velocity dispersion: star clusters show no need for dark matter, while ultrafaint dwarfs generally appear to need a lot. This of course assumes that their measured velocity dispersions represent an equilibrium measure of their gravitational potential, which is what we’re questioning here, so the opportunity for circular reasoning is rife.
$Rather than apply a strict luminosity cut, for convenience I’ve kept the same “not safe from tidal disruption” distinction that we’ve used before. Some of the objects in the 105 – 106 M☉ range might belong more with the classical dwarfs than with the ultrafaints. This is a reminder that our nomenclature is terrible more than anything physically meaningful.
&Astronomy is an observational science, not a laboratory science. We can only detect the photons nature sends our way. We cannot control all the potential systematics as can be done in an enclosed, finite, carefully controlled laboratory. That means there is always the potential for systematic uncertainties whose magnitude can be difficult to estimate, or sometimes to even be aware of, like how local variations impact Jeans analyses. This means we have to take our error bars with a grain of salt, often such a big grain as to make statistical tests unreliable: goodness of fit is only as meaningful as the error bars.
I say this because it seems to be the hardest thing for physicists to understand. I also see many younger astronomers turning the crank on fancy statistical machinery as if astronomical error bars can be trusted. Garbage in, garbage out.
*This is an example of setting a parameter in a model “by hand.”
**The transition to thinking in terms of the luminosity function rather than Tully-Fisher is so complete that the most recent, super-large, Euclid flagship simulation doesn’t even attempt to address the kinematics of individual galaxies while giving extraordinarily detailed and extensive details about their luminosity distributions. I can see why they’d do that – they want to focus on what the Euclid mission might observe – but it is also symptomatic of the growing tendency to I’ve witnessed to just not talk about those pesky kinematics.
%Halos in dark matter simulations tend to be rather triaxial, i.e., a 3D bloboid that is neither spherical like a soccer ball nor oblate like a frisbee nor prolate like an American football: each principle axis has a different length. If real halos were triaxial, it would lead to non-circular orbits in dark matter-dominated galaxies that are not observed.
The triaxiality of halos is a result from dark matter-only simulations. Personally, I suspect that the condensation of gas within a dark matter halo (presuming such things exist) during the process of galaxy formation rounds-out the inner halo, making it nearly spherical where we are able to make measurements. So I don’t see this as necessarily a failure of LCDM, but rather an example of how more elaborate simulations that include baryonic physics are sometimes warranted. Sometimes. There’s a big difference between this process, which also compresses the halo (making it more dense when it already starts out too dense), and the various forms of feedback, which may or may not further alter the structure of the halo.
^There are many failure modes in simulated rotation curves, the two most common being the cusp-core problem in dwarfs and sub-maximal disks in giants. It is common for the disks of bright spiral galaxies to be nearly maximal in the sense that the observed stars suffice to explain the inner rotation curve. They may not be completely maximal in this sense, but they come close for normal stellar populations. (Our own Milky Way is a good example.) In contrast, many simulations produce bright galaxies that are absurdly sub-maximal; EAGLE and SIMBA being two examples I remember offhand.
Another common problem is that LCDM simulations often don’t produce rotation curves that are as flat as observed. This was something I also found in my early attempts at model-building with dark matter halos. It is easy to fit a flat rotation curve given the data, but it is hard to predict a priori that rotation curves should be flat.
!!Gravitational lensing indicates that rotation curves remain flat to even larger radii. However, these observations are only sensitive to galaxies more massive than those under discussion here. So conceivably there could be another coincidence wherein flatness persists for galaxies with Mb > 1010 M☉, but not those with Mb < 109 M☉.
!!!Many in the community seem to agree that it will surely work out.
##I’ve tried to estimate dissolution timescales, but find the results wanting. For plausible assumptions, one finds timescales that seem plausible (a few Gyr) but with some minor fiddling one can also find results that are no-way that’s-too-short (a few tens of millions of years), depending on the dwarf and its orbit. These are crude analytic estimates; I’m not satisfied that these numbers were particularly meaningful. Still, this is a worry with the tidal-stirring hypothesis: will perturbed objects persist long enough to be observed as they are? This is another reason we need detailed simulations tailored to each object.
*&^#Note added after initial publication: While I was writing this, a nice paper appeared on exactly this issue of the star formation history of a good number of ultrafaint dwarfs. They find that 80% of the stellar mass formed 12.48 ± 0.18 Gyr ago, so 12.5 was a good guess. Formally, at the one sigma level, this is a little after reionization, but only a tiny bit, so close enough: the bulk of the stars formed long ago, like a classical globular cluster, and these ultrafaints are consistent with being fossils.
Intriguingly, there is a hint of an age difference by kinematic grouping, with things that have been in the Milky Way being the oldest, those on first infall being a little younger (but still very old), and those infalling with the Large Magellanic Cloud a tad younger still. If so, then there is more to the story than quenching by cosmic reionization.
They also show a nice collection of images so you can see more examples. The ellipses trace out the half-light radii, so can see the proclivity for many (not all!) of these objects to be elongated, perhaps as a result of tidal perturbation:
Figure 2 from Durbin et al. (2025): Footprints of all HST observations (blue filled patches) overlaid on DSS2 imaging cutouts. Open black ellipses show the galaxy profiles at one half-light radius.