Mastodawn

New paper!

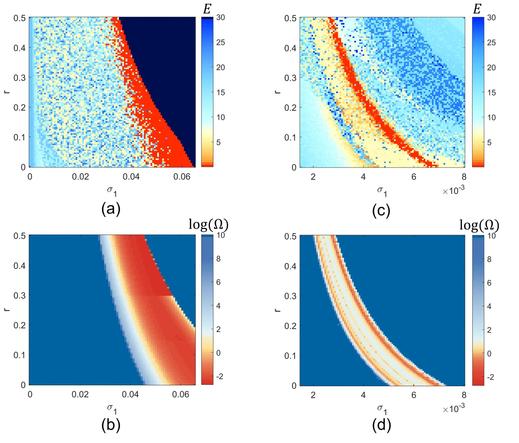
If you want to assess the stability of the synchronization of a system of identical oscillators, you can use the Master Stability Function. However, what do you do in a real-world case, when the elements of the system are not exactly identical? We show how to extend the formalism and use it also when there are many-body interactions, such as in a simplicial complex.

https://journals.aps.org/prresearch/abstract/10.1103/ml7b-r35h

#mathematics #physics #science #synchronization #stability #chaos #MSF #simplicialcomplex #complexity #nonlinear #dynamics

Show thread

Charo del Genio Apr 10

If you don't have access to the journal, you can download it from here

https://charodelgenio.weebly.com/recon.html

#physics #mathematics #networks #reconstruction #higherorder #simplicialcomplex #hypergraphs #evolutionarygames #transient #dynamics #algorithm

Reconstructing simplicial complexes from evolutionary games

CHARO DEL GENIO

Show thread

Charo del Genio Apr 10

The paper is on Physical Review E

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.111.044304

#physics #mathematics #networks #reconstruction #higherorder #simplicialcomplex #hypergraphs #evolutionarygames #transient #dynamics #algorithm

Charo del Genio Apr 10

New paper, just out.

Often, in real-world situations, one does not know the full structure of a network. However, at the same time, one can often observe some interactions that take place on it, and may be interested in knowing its full structure. For example, one may be detecting some partial criminal activity and may want to determine the whole organization. We consider higher-order networks, which are structures with many-body interactions, and specifically simplicial complexes, and show that one can reconstruct a whole network almost perfectly simply by observing the transient of the dynamics that takes place on it. In fact, we give 3 different algorithms to do it, with different complexities and accuracies, so you can choose which one suits you best.

#physics #mathematics #networks #reconstruction #higherorder #simplicialcomplex #hypergraphs #evolutionarygames #transient #dynamics #algorithm

AlexCrimi Mar 23

#simplicialcomplex + #Causality +#Reservoircomputing:
"Higher-order Granger reservoir computing: simultaneously achieving scalable complex structures inference and accurate dynamics prediction" https://www.nature.com/articles/s41467-024-46852-1

#dynamicalsystem #ML #AI

Higher-order Granger reservoir computing: simultaneously achieving scalable complex structures inference and accurate dynamics prediction - Nature Communications

For reservoir computing, improving prediction accuracy while maintaining low computing complexity remains a challenge. Inspired by the Granger causality, Li et al. design a data-driven and model-free framework by integrating the inference process and the inferred results on high-order structures.

Nature

MottG Feb 8

It would be interesting if someone used simplicial complex techniques from topology to analyze Wikipedia, or even developed tools for end users to
apply simplicial complexes to Wikipedia queries. The following papers illustrate what you can do with them.

"Co-occurrence simplicial complexes in mathematics: identifying the holes of knowledge"
https://appliednetsci.springeropen.com/articles/10.1007/s41109-018-0074-3

"The shape of collaborations"
https://www.semanticscholar.org/paper/The-shape-of-collaborations-Patania-Petri/e00b3707885b94647619d66147dda40363fd090e

#Wikipedia #TDA #simplicialCOmplex

Co-occurrence simplicial complexes in mathematics: identifying the holes of knowledge - Applied Network Science

In the last years complex networks tools contributed to provide insights on the structure of research, through the study of collaboration, citation and co-occurrence networks. The network approach focuses on pairwise relationships, often compressing multidimensional data structures and inevitably losing information. In this paper we propose for the first time a simplicial complex approach to word co-occurrences, providing a natural framework for the study of higher-order relations in the space of scientific knowledge. Using topological methods we explore the conceptual landscape of mathematical research, focusing on homological holes, regions with low connectivity in the simplicial structure. We find that homological holes are ubiquitous, which suggests that they capture some essential feature of research practice in mathematics. k-dimensional holes die when every concept in the hole appears in an article together with other k+1 concepts in the hole, hence their death may be a sign of the creation of new knowledge, as we show with some examples. We find a positive relation between the size of a hole and the time it takes to be closed: larger holes may represent potential for important advances in the field because they separate conceptually distant areas. We provide further description of the conceptual space by looking for the simplicial analogs of stars and explore the likelihood of edges in a star to be also part of a homological cycle. We also show that authors’ conceptual entropy is positively related with their contribution to homological holes, suggesting that polymaths tend to be on the frontier of research.

SpringerOpen