The previous demo made me dig deeper into dithering algorithms. It's something I should have done years ago, as I've been using simple random dithering now and then, and I hadn't even thought of gamma correction. One algorithm in particular caught my eye: Riemersma dithering, which uses the Hilbert curve. Compared to the usual matrices for error diffusion, the curve approach seemed easier to implement in some ways, as it has fewer edge issues.

More interestingly, it struck a chord with my earlier experiments with space-filling curves in image processing. So it was a kind of familiar territory, but it also seemed esoteric enough that I could imagine making some new discoveries. For example, play with other plane-filling curves besides the Hilbert.

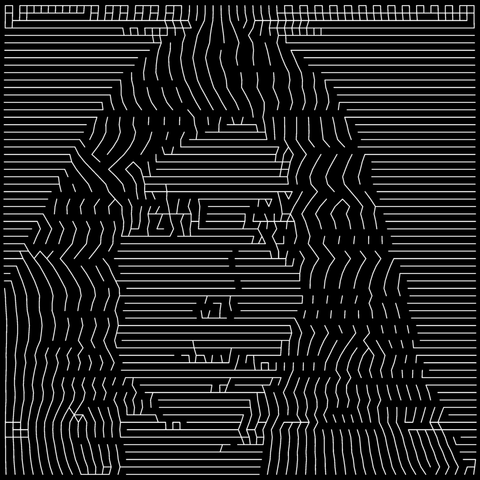
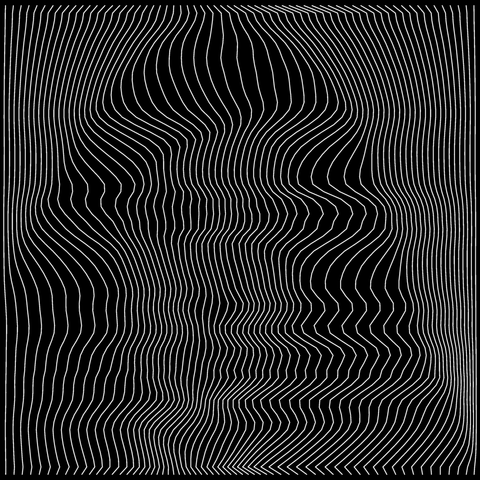
The first image uses the boustrophedon curve, which makes the vertical wave patterns I recall from a number of non-dithering demos. The second curve is what I call the diagstrophedon, a diagonal zig-zag starting from the top left corner, and I think its wavy artefacts make a nice match for Venus's hair.

Then in image 3 we have Hilbert, which doesn't seem to make any particular artefacts, and I guess that's a good thing for dithering. Finally 4 uses the Peano curve, which makes some fun wiggles in light areas.

#dithering #riemersmadithering #stippling #halftoneart #raster #pixelart #hilbertcurve #peanocurve #planefillingcurve #spacefillingcurve #pythoncode #opengl #algorithmicart #algorist #mathart #laskutaide #ittaide #kuavataide #iterati

Yet another optimized Voronoi tiling. This was supposed to be a simpler alternative to the previous tiling approach, but I ended up going down a rabbit hole of various dithering algorithms.

Instead of the equal-sum partitions, this uses regular dithering to find the Voronoi seed points, and the tile areas are inversely proportional to the colour values. My simple random dithering didn't work as well as expected, so I started to look into alternatives. I was of course aware of Floyd-Steinberg, and as I grew a bit tired of this demo, I ended up cheating a little by using a ready-made library. Since I was using PIL for image handling anyway, I could simply use its format conversion functions to get a 1-bit image, which uses F-S by default.

As before, I planned to use edge detection to get smaller tiles at the contrast edges. However, it didn't work so well with dithering, as it would concentrate basically all seed points at the edges. So here I used a mix of edge detection and the original. I think it worked out nicely here, as the bright colours often coincide with areas of small detail, while the dark background doesn't need much resolution.

#voronoidiagram #pixelart #blockart #tiling #raster #mosaic #pythoncode #opengl #algorithmicart #algorist #mathart #laskutaide #ittaide #kuavataide #iterati

I wanted to make the optimized tiling look more organic, and I've already played with Voronoi diagrams quite a lot. But this turned out a bit more messy than expected. To preserve the size and shape variations of the rectangles in the Voronoi cells, I ended up using a non-uniformly weighted metric. I guess it counts as a shape metric, using the definition in my Bridges 2020 paper.

As before, there's a roughly uniform tiling with an equal number of cells for comparison.

#voronoidiagram #pixelart #blockart #tiling #raster #mosaic #pythoncode #opengl #algorithmicart #algorist #mathart #laskutaide #ittaide #kuavataide #iterati

Another visual refinement to a recent demo: adding seams to the optimized tiling scheme. While it breaks the mosaic illusion to some extent, I think it makes the tile sizing idea much clearer. As before, there's a uniform variant with the same number of tiles for comparison.

Source photo: Mary of Egypt by José de Ribera, in public domain.

#pixelart #blockart #tiling #raster #mosaic #pythoncode #opengl #algorithmicart #algorist #mathart #laskutaide #ittaide #kuavataide #iterati

How it was supposed to look like in the first place: rounded with Bezier curves.

I've used Bezier curves and Hermite splines quite a lot to smooth out progressions of discrete points, such as Hamiltonian circuits. The challenge with this Hilbert curve is that there are tens of thousands of points, so drawing a nice OpenGL shape for each edge gets rather slow. Of course, this isn't a deal breaker for still images, but I like making my code efficient.

I've now constructed the Bezier curves in geometry shaders. I've used those for some time to draw simpler shapes more efficiently, such as line segments with rounded ends; the idea is to do more work on the GPU, while moving as little data as possible there. These line segments only need the endpoint coordinates, as well as thickness and colour. The curves seemed more challenging due to the number of parameters, but in the end there weren't really any issues.

#beziercurve #hilbertcurve #planefillingcurve #spacefillingcurve #lineart #linedrawing #singlelinedrawing #pythoncode #opengl #geometryshader #algorithmicart #algorist #mathart #laskutaide #ittaide #kuavataide #iterati

The recent stipplings and partitionings reminded me of this demo from about 2 years ago. In short, it's a Hilbert curve where the iteration level varies by the colour value. I wanted to make some small changes, but I ended up rewriting it completely. The shader approach seemed needlessly heavy and redundant for something that works more naturally on a CPU. But mostly it was just a fun exercise in looking at the same problem from a different angle.

The first picture shows the original idea. With the new idea, I wanted to get rid of the slanted lines; the result doesn't feel any better to me, but I guess it's interesting in its own way.

#hilbertcurve #planefillingcurve #spacefillingcurve #lineart #linedrawing #singlelinedrawing #pythoncode #opengl #algorithmicart #algorist #mathart #laskutaide #ittaide #kuavataide #iterati

I came across this halftoning idea sometime last week. While the idea was relatively easy to understand and fun to implement, I've spent quite a lot of time trying to make the result look nice.

In each row, the image is split into bins containing roughly the same sum of lightness value. This is nice to implement when the number of lines/bins is a power of 2, so we can recurse with a binary split. Thus the line density varies by average lightness. The problem is that density is considered along the x-axis. If things change a lot between rows, the lines get slanted, so they appear more dense. Here I've included some averaging between neighbouring rows to make thing a bit smoother.

I'm also including a fun glitch from the early tests. The line-density system includes the set of point coordinates and the graph structure (which point is connected to which). What happened here is my generic graph generator that simply finds the nearest neighbours of each point. So in the light areas that are compressed horizontally, the nearest neighbours were left and right.

#halftoneart #lineart #patterns #texture #pythoncode #opengl #algorithmicart #algorist #mathart #laskutaide #ittaide #kuavataide #iterati

I've always found circuit boards aesthetically inspiring, and in recent years this fascination has turned into a number of PCB-styled demos. I think a key inspiration for these has been the "Absolut Intelligence" vodka advert a couple of decades ago.

I haven't done these in a while, but a week or two ago I ran into spanning trees. I noticed that spanning trees of square lattices can make rather nice impersonations of printed circuits, especially when the solder points are only put on leaf points. Cut the tree up into a forest, and it's making even more electrical sense.

Halftoning isn't new to me either, but my existing line-based techniques didn't look nice on the square PCB lattice. It had to be more blocky with exactly horizontal or vertical lines. So for this iteration, I've set each half-edge to have a constant width — a natural evolution of my earlier variants, which were built from half-edge sections. Of course, the solder points follow a similar areal scaling.

#absolutintelligence #spanningforest #spanningtree #circuitboardart #pcbart #electronicsart #patterns #texture #pythoncode #opengl #algorithmicart #algorist #mathart #laskutaide #ittaide #kuavataide #iterati

Minimum spanning tree of a dithered image, 4096 vertices. Model: Swetlana

#spanningtreeyoungandsweet #minimumspanningtree #primsalgorithm #graphtheory #halftoneart #lineart #pythoncode #opengl #algorithmicart #algorist #mathart #laskutaide #computerart #ittaide #kuavataide #iterati