Chris Wolff 
Wonder of ScienceFurther reading: https://en.wikipedia.org/wiki/Tennis_racket_theorem
Murdoc Addams 🧛🏻
🇨🇦@wonderofscience
The article said I could do it with a remote control, so I did. In 9 tries, it did the flip in all but 1. Weird. 😳
The article said I could do it with a remote control, so I did. In 9 tries, it did the flip in all but 1. Weird. 😳
Mister Wanko@wonderofscience i can do it throwing an axe.
KanaMaunaScrew going to Mars. This is what mankind was made for.
Hey Gus@wonderofscience the strangest part is how moment develops due to the unstable axis. The second loop really highlights it how there’s a constant (visually) increase in distance on each set of rotations. Super neat!
Eryngium@wonderofscience #AltText #Alt4You A silver T-shaped handle sticks out of a white wall along with other assorted dials. A person spins the handle counterclockwise so that the top of the T spins parallel to the wall. As it spins, the handle detaches itself from the wall and hovers spinning in the air in zero-gravity. For every few rotations of the top of the T, the entire handle flips direction, so that the part that had been attached to the wall now points away from the wall, and then flips back again. The same phenomenon is then replayed in slow motion from a different angle.
David Croyle@wonderofscience That's all kinds of awesome!
Flaming Cheeto@wonderofscience matrix be broken
MegatronicThronBanksLooks like a Chaos effect.
Also. This says to me that when we write computer game physics, we should not try to script the object's *movement*, we should always try to script its *components* from first principles. That way, apart from minor collisions not flipping the horse and cart into the stratosphere (cough), we might actually once in a while get to see real world unexpected effects.
ALT TEXT (this is all off the cuff and I'm typing this on my phone; no ChatGPT, no Google, no nothing; please correct anything I may have wrong here, or worded funny, etc.):
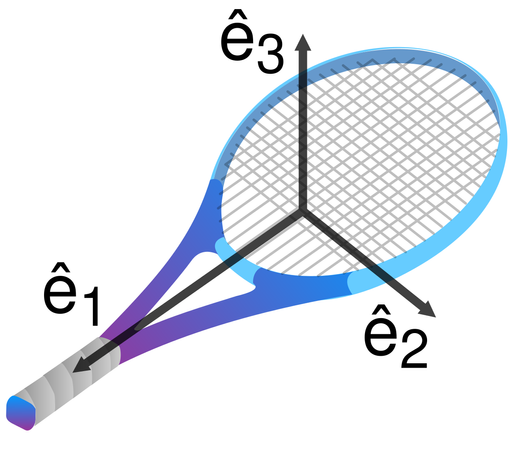
The video shows by demonstration a really cool behavior of objects in motion, understood to the study of physics according to intermediate axis theorem—also called tennis racket theorem, or the Dzhanibekov effect. We see an astronaut spin a T shaped handle that is attached to a control panel, and it unscrews from the panel, as one would expect. Curiously, the handle—which is, unsurpisingly, floating due to this happening in space—continues to spin while facing the same way with respect to the panel as it did initially, only briefly; it then flips around 180° in said direction, such that the horizontal section where it's meant to be grabbed in order to use it, is then facing towards the panel instead of away from it. This orientation then reverses again, and then reverses again, and so on and so forth, repeatedly. Like that weren't enough, it just keeps spinning the same way it was already spun by the astronaut, while doing the other thing that was just described (taken into account that it turns itself around going the other way whenever it does, of course). The reason why this is called intermediate axis theorem is because all objects with mass, while in motion, will always rotate upon whichever axis provides the highest moment of inertia no matter what, unless otherwise acted upon by an outside force; this axis is, of course, the intermediate axis. The reason why this is also called tennis racket theorem is because it is observed while fully affected by gravity, by throwing a tennis racket end-over-end directly upwards: it is physically impossible for it to rotate upon said axis without also rotating upon the axis 90° perpendicular, and it will have already rotated upon the latter to such extent by the time whoever threw it has had a chance to catch it by the handle again, that the net will no longer be facing in quite the same direction it was when it was thrown. The author of this alt text assumes that Dzhanibekov is most likely who first discovered this, or something, although he doesn't remember offhand and doesn't feel like looking it up. He was taught K-12 at home by a former private school teacher and never went to school in a conventional sense, he earned his GED in 2011 at the age of 17, and he has precisely no qualifications otherwise.
🇨🇦️Dracula🍁@wonderofscience The video isn't playing for me apparently because the file is corrupt. 
Jon Sullivan@countdracula @wonderofscience It's working for me. 🤷
Alistair K@joncounts @countdracula @wonderofscience You can see and hear Dzhanibekov himself talk about it here: https://www.youtube.com/watch?v=dL6Pt1O_gSE
Let me know if you understand what the potato-with-a-threaded-nut is about half-way through.
джанибеков
@libroraptor @joncounts @wonderofscience Actually, I can't. This is what I get when I try at Youtube.
@countdracula @joncounts @wonderofscience fascinating! I'm in New Zealand, in case that explains a difference of access.
@countdracula @joncounts @wonderofscience Does this link get you there? (Well, technically somewhere else, but it should look and sound the same.) https://yewtu.be/watch?v=dL6Pt1O_gSE
@libroraptor @countdracula @wonderofscience Thanks. I love how Dzhanibekov demonstrates it with a potato. Very Russian. Veritasium has a good explanation of the effect too. That threaded nut on the potato is needed to make that third axis of rotation unstable (moment of inertia).
The Veritasium video covers some of the history of the effect and how Russians kept the effect in space secret for a decade.
Fascinating stuff.
The Bizarre Behavior of Rotating Bodies
@libroraptor @countdracula @wonderofscience Sadly, Veritasium mentions that the spinning brown blob was clay, not a Russian potato. Someone on the space station needs to do it with a potato.
@joncounts @countdracula @wonderofscience Oh, well if it's only clay, then it's not interesting any more :(
@joncounts @countdracula @wonderofscience It's the potato rather than the threaded nut that fascinates me, indeed more than the precession and flipping. I've just been sitting here thinking of all the physics textbooks I've read (both as a physicist and as an historian of science) and cannot recall even one potato in any of them.
@libroraptor @countdracula @wonderofscience I know! It's a travesty. Surely there's a huge market out there for books on the physics of potatoes. 😄
@libroraptor @countdracula @wonderofscience It looks like I spoke too soon. I searched and it turns out #PotatoPhysics is a thing!
Dr. Tatiana Does Potato Physics! | Physics in Minutes
@joncounts @countdracula @wonderofscience Just like setting the blade of a coffin plane!
Her accent is a big asset here. American flamboyance isn't a bad thing in lecturing either, but I can take it only in small doses.
Worik@libroraptor @joncounts @countdracula @wonderofscience
I spent years studying pointy headed economics and finance. There is much "physics envy" in economics...
But we used "potatoes" as unit of currency in theoretical finance. So score one! Physics can kiss my econometric arse!!
Never, ever, thought I would be able to say that. Thank you
@joncounts @libroraptor @wonderofscience With opensuse tumbleweed and both Firefox and Vivaldi, there was no audio with this video. However, with Linux Mint and Firefox, the audio was there. The first video still yaps about the copyright thing.
I guess I make changes to avoid this. I was thinking about changes anyway. Not tonight, though. The joys of electronics.
I guess I make changes to avoid this. I was thinking about changes anyway. Not tonight, though. The joys of electronics.
@countdracula @joncounts @wonderofscience I noticed on Invidious that instances in North America got the copyright block. Some others say that the media can't be played for various reasons that I don't pay much attention to. It can take me a few tries to find one that plays.
@libroraptor I can understand it being done for licensing/copyright issues. Otherwise, it almost sounds like some don't think people elsewhere might be interested. The general consensus, from what I've read, seems to be to use a VPN. Oh well. Stuff happens, I guess.
itsFriday@joncounts @libroraptor @countdracula @wonderofscience What is the name of the russian movie he mentiones?
@itsFriday @joncounts @countdracula @wonderofscience Could you direct us with a timepoint? (It's a long video that I don't have patience and brainpower to search through....)
@libroraptor @joncounts @countdracula @wonderofscience In the first minute.
Found it meanwhile: https://en.m.wikipedia.org/wiki/Salyut_7_(film)
Thanks!
Found it meanwhile: https://en.m.wikipedia.org/wiki/Salyut_7_(film)
Thanks!
Robin@wonderofscience fascinating
Karsten@wonderofscience do you by chance know what machine the handle is detached from?
Steve's Place@byteborg @wonderofscience It looks like it says Outer Pellet Storage System Door. Whether the handle is functionally part of it, or is just there to run the experiment you see, I am unaware of.
Bill, organizer of stuff@wonderofscience I always marvel at this when I flip and catch a hammer.
skuaMemo
When designing an orbital ring habitat, do be sure to have the axial complex positioned to only one side of the ring.
🇨🇦🇩🇪🇨🇳张殿李🇨🇳🇩🇪🇨🇦@wonderofscience Something about this behaviour reminds me of Tippe Tops. Not quite the same, but ... kissing cousins maybe?