了解计算思维如何让你做到一切尽在掌握中。
我们身处的这个世界联系越来越 紧密、 越来越可配置, 越来越可计算、越来越可编程。你可以一直做个被动的参与者,等你能写代码时,你就是导演,你就是创造者,你能指挥那些计算机 ,让它们做你希望它们做的事情。如果你能写代码,你就能控制自己的命运(或者至少能编写你自己的联网草坪洒水系统) 。不过,如何学习写代码呢?首先要学着用计算机的方式思考问题 。其次,你要学握一门编程语言,可以与你的计算机、移动设备或者任何有CPU的 设备讲同样的语言。
这对你有什么好处呢? 你的能力会更强,更有创造力,而且会有更多的时间来做你真正想做的事情。来吧,现在就开始……
分解
在写你的第一段代码之前,首先面对的就是要掌握一种分解技能,要能够将问题分解为计算机可以实现的小动作。当然,你和计算机还要讲同一种共同的语言,不过这个内容稍后再做介绍。
要把一个问题分解为一系列步骤,听上去这好像是个新的技能,但实际上这就是你每天都会做的事情。下面来看一个简单的例子:假设你想把钓鱼过程分解为一组简单的指令,然后把这组指令交给一个机器人,让它为你钓鱼。我们首先会这么做:
1. 在鱼钩上放虫子
2. 把鱼线甩入池塘 (有些步骤只是简单的指令,或者可以成为「语句」)
3. 观察浮标,直到浮标沉入水里 (语句会有条件地等待,要用到 if ,然后继续执行)
4. 收线把鱼儿拉上来 (等上一个语句中的浮标沉进水里,才可以执行这个语句)
5. 如果结束钓鱼,则回家;否则,再回到第1步。(语句还可以做「决定」,比如继续钓鱼还是回家。语句经常重复,就是循环,就像这样:如果我们不回家,就再回到最前面,重复这些指令就能再钓一条鱼)
我们可以把这些语句看作是钓鱼的一个秘诀或做菜的一个食谱。与所有食谱一样,这里提供一组步骤,如果按顺序完成这个步骤,会得到某个结果(在这里就是钓到鱼)。
注意大多数步骤都是一简单的指令,比如“把鱼线甩入池塘”或者“收线把鱼拉上来”。不过要注意,另外一些指令却有些不同,因为它们取决于一个条件,比如“浮标在水上还是在水下?”指令还可以指示流程,比如“如果还要继续钓鱼,就回到最前面,再在鱼钩上面放一条虫子”。或者,也可能是一个停止条件,比如“如果结束钓鱼,就回家”。
你会发现这些简单语句或指令正正是编写代码的基础。实际上,你使用的所有软件其实都是写给计算机的一组简单指令(有时候有几十万行那么多),它们会告诉计算机要做什么。
实际上,用食谱(recipe)来描述那些写给计算机看的指令是很合适的。在更高级的编程书里,你会经常看到这个词语。要知道,一些关于软件开发技术的书的书名使用了cookbook(这个词本意同样是食谱,通常引申地表示这是一本操作手册)。尽管如果,如果你想看起来更有技术含量,我们也会满足你,计算机科学家或更严谨的软件开发人员通常会把这样的一个食谱成为算法(algorithm)。什么是算法?嗯,其实与食谱差不多,就是一堆指令。可以解决某个问题的指令序列。你会经常看到算法被写成一种非正式的代码,这种代码被称为伪代码(pseuducode)。
有一点要记住,不论你在谈论一个食谱、伪代码还是算法,关键是:在写计算机能理解能执行的代码之前,先不要过分深究具体的细节,应当首先得出如何解决问题的一个高级描述。
在这本书中,你会看到我们交替地使用这些术语。在适当的情况下,例如你在下次参加面试时,使用算法或伪代码可能会更好一些,这样可能会给你更好的薪水。因为算法或伪代码的说法显得更内行,不过食谱这个词也没有错。
以上内容出自《HeadFirst编程之旅 python语言描述》
#算法 #cookbook #python #编程 #HeadFirst编程之旅
🌘 雜湊表封裝問題
➤ 魔法位元板優化的理論瓶頸
✤ https://backscattering.de/chess/hashtable-packing/
本文探討了雜湊表封裝問題的計算複雜度,證明其為強 NP-完全問題。此問題源於國際象棋編程中優化魔法位元板(Magic Bitboards)的過程。證明表明,不存在多項式時間算法,甚至偽多項式時間算法或多項式時間近似方案來尋找最佳解,因此實務上應採用啟發式演算法。儘管如此,作者也指出,針對特定情境(如國際象棋魔法位元板的應用),可能存在尚未發現的有效解決方案。
+ 這篇文章深入探討了一個非常具體的計算問題,但卻揭示了更廣泛的理論侷限性,讓人印象深刻。
+ 對於不熟悉國際象棋或魔法位元板的人來說,理解文章需要一些背景知識,但其核心的計算複雜度論證仍然很有價值。
#計算機科學 #算法 #複雜度理論 #國際象棋
➤ 魔法位元板優化的理論瓶頸
✤ https://backscattering.de/chess/hashtable-packing/
本文探討了雜湊表封裝問題的計算複雜度,證明其為強 NP-完全問題。此問題源於國際象棋編程中優化魔法位元板(Magic Bitboards)的過程。證明表明,不存在多項式時間算法,甚至偽多項式時間算法或多項式時間近似方案來尋找最佳解,因此實務上應採用啟發式演算法。儘管如此,作者也指出,針對特定情境(如國際象棋魔法位元板的應用),可能存在尚未發現的有效解決方案。
+ 這篇文章深入探討了一個非常具體的計算問題,但卻揭示了更廣泛的理論侷限性,讓人印象深刻。
+ 對於不熟悉國際象棋或魔法位元板的人來說,理解文章需要一些背景知識,但其核心的計算複雜度論證仍然很有價值。
#計算機科學 #算法 #複雜度理論 #國際象棋
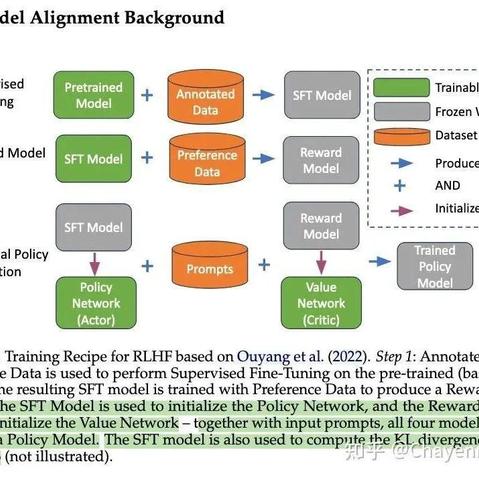
淺析主流 Alignment 算法與 NeMo-Aligner 框架
https://www.headline01.com/a/jjgYL-vEjNty0rMTm6GGlg-5FD6AC9C.html
#框架 #算法
https://www.headline01.com/a/jjgYL-vEjNty0rMTm6GGlg-5FD6AC9C.html
#框架 #算法
🌗 估算對數 - Niklas Oberhuber
➤ 重拾對數的藝術:一種古老而精妙的估算方法
✤ https://obrhubr.org/logarithm-estimation
本文介紹了約翰·納皮爾在1615年左右開發的一種估算以10為底的對數的簡便方法。該方法基於對數的特性,利用數字的位數來近似對數值,並結合科學記號法進行迭代計算,以提高精度。作者分享了其Python腳本實現,並鼓勵讀者查閱Charles Petzold的《對數的失落藝術》以獲取更多資訊。
+ 這篇文章讓我重新思考了對數的本質,也讓我對早期數學家的智慧感到敬佩。
+ 雖然方法看起來有些繁瑣,但作者提供的Python程式碼讓實現起來變得更簡單了,真是不錯的分享!
#科學 #數學 #對數 #算法
➤ 重拾對數的藝術:一種古老而精妙的估算方法
✤ https://obrhubr.org/logarithm-estimation
本文介紹了約翰·納皮爾在1615年左右開發的一種估算以10為底的對數的簡便方法。該方法基於對數的特性,利用數字的位數來近似對數值,並結合科學記號法進行迭代計算,以提高精度。作者分享了其Python腳本實現,並鼓勵讀者查閱Charles Petzold的《對數的失落藝術》以獲取更多資訊。
+ 這篇文章讓我重新思考了對數的本質,也讓我對早期數學家的智慧感到敬佩。
+ 雖然方法看起來有些繁瑣,但作者提供的Python程式碼讓實現起來變得更簡單了,真是不錯的分享!
#科學 #數學 #對數 #算法
🌘 隱藏子羣問題
➤ 量子計算的基礎與應用:探索隱藏子羣問題的本質
✤ https://www.daniellowengrub.com/blog/2025/04/23/hidden-subgroup
本文介紹了隱藏子羣問題 (HSP),它是一個比整數因式分解和離散對數問題更普遍的問題。這兩種著名的量子算法,即 Shor 算法,都可以視為 HSP 的特例。當羣是阿貝爾羣時,存在一種標準方法可以有效解決 HSP。文章探討了 HSP 在兩個重要實例中的應用:Simon 問題和離散對數問題,並展示瞭如何將它們轉化為 HSP 的形式,從而可以利用 Shor 算法進行解決。
+ 這篇文章清楚地說明瞭隱藏子羣問題的重要性,並解釋了它與密碼學的關聯性。對於想要了解量子計算的基礎知識的人來說,是一篇很好的入門文章。
+ 文章深入探討了 HSP 的數學細節,雖然有些難度,但對於專業人士來說,可以提供更深入的理解。
#量子計算 #密碼學 #算法
➤ 量子計算的基礎與應用:探索隱藏子羣問題的本質
✤ https://www.daniellowengrub.com/blog/2025/04/23/hidden-subgroup
本文介紹了隱藏子羣問題 (HSP),它是一個比整數因式分解和離散對數問題更普遍的問題。這兩種著名的量子算法,即 Shor 算法,都可以視為 HSP 的特例。當羣是阿貝爾羣時,存在一種標準方法可以有效解決 HSP。文章探討了 HSP 在兩個重要實例中的應用:Simon 問題和離散對數問題,並展示瞭如何將它們轉化為 HSP 的形式,從而可以利用 Shor 算法進行解決。
+ 這篇文章清楚地說明瞭隱藏子羣問題的重要性,並解釋了它與密碼學的關聯性。對於想要了解量子計算的基礎知識的人來說,是一篇很好的入門文章。
+ 文章深入探討了 HSP 的數學細節,雖然有些難度,但對於專業人士來說,可以提供更深入的理解。
#量子計算 #密碼學 #算法