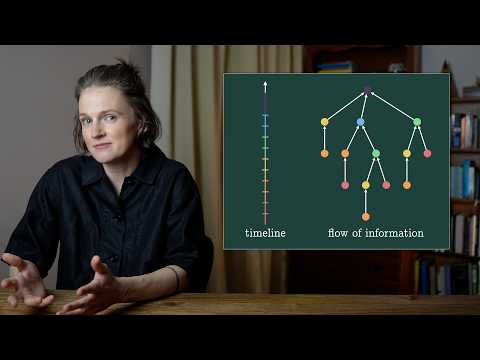
“Tree Evaluation Is in Space 𝑂 (log 𝑛 · log log 𝑛)”
‘The #TreeEvaluation #Problem (TreeEval) (Cook et al. 2009) is a central candidate for separating polynomial time (P) from logarithmic space (L) via composition. While space lower bounds of Ω(log2 n) are known for multiple restricted models, it was recently shown by #Cook and #Mertz (2020) that TreeEval can be solved in space O(log2 n/loglogn). Thus its status as a candidate hard problem for L remains a mystery.
Our main result is to improve the space complexity of #TreeEval to O(logn · loglogn), thus greatly strengthening the case that Tree Evaluation is in fact in L. We show two consequences of these results. First, we show that the #KRWconjecture (#Karchmer, #Raz, and #Wigderson 1995) implies L ⊈NC1; this itself would have many implications, such as branching programs not being efficiently simulable by formulas’