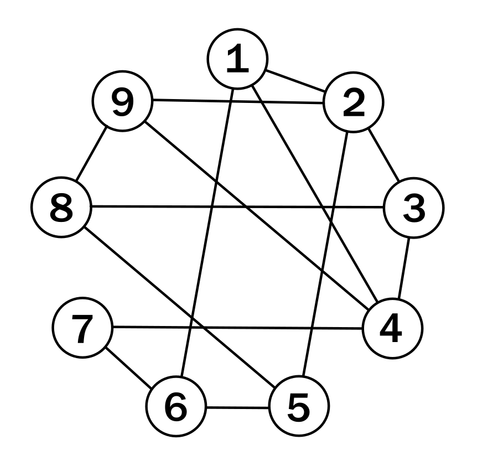
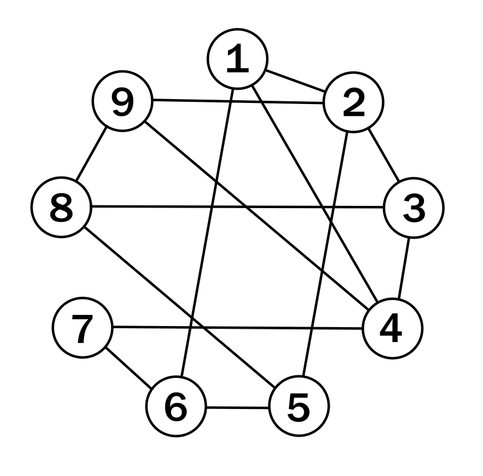
Today's random thing: got myself thinking about this graph of pairs of digits 1-9 that produce prime sums. Much sparser than the complementary graph of pairs that sum to composite numbers, which I sort of knew would be true but hadn't ever examined up close.
I enjoy the resulting asymmetrical sigil, and how each distinct prime that can be summed to ends up having its own consistent slope among the diagonal connections: all 11s, all 13s, all 7s, all 5s.
Inspiration for this is a fiendishly difficult sudoku variant puzzle, that Simon from Cracking the Cryptic spent four hours solving (he burns through most in 40 minutes or so including generous explanation), and it involves accounting for whether any two adjacent digits in the puzzle do or do not add to a prime value.
In trying to figure out how to start, I got curious about the distribution of prime vs. composite sums.
Puzzle video, if you're curious/masochistic: https://www.youtube.com/watch?v=vMdx3kmNFh4
Part of my thought was, okay, maybe I can find some helpful constraints in the puzzle if it turns out to be hard to string either multiple prime sums or multiple composite sums together on a single line (which, by Sudoku rules, will only contain each digit 1-9 exactly once).
A way to frame that is, how long of a walk can you do on a connected graph of adjacent digits without revisiting any nodes?
Unfortunately, the answer is "a real long one" , which makes this not much of a constraint.
You can see in the graph that most nodes have at least three paths to other nodes; 7 is the only one with fewer, with only two connections, to 4 and to 6.
It's not hard to find a way to do a full walk of the graph, visiting every single node, e.g.:
1, 2, 3, 4, 9, 8, 5, 6, 7
What that translates to for Sudoku is that you could put those digits in that sequence in a single row or column and no two adjacent digits would sum to a composite number. Ah, well, drat.
(There's an easy thought experiment behind why I'd already assumed there'd be fewer prime sums than composite sums here:
1. Every odd + odd pair, and every even + even pair, will lead to an even number. And with the exception of 2, all even numbers are composite.
2. That accounts for roughly half of the digit combos you can make. The other half are an odd + even pair, which results in an odd sum.
3. Not all odd numbers are prime! e.g. 3+6 and 4+5 both give us 9, which is 3*3. )
Here's an interesting little detail: no three nodes on this graph are a fully connected subgraph -- that is, for any three nodes, it's not the case that A-B and B-C and A-C are all edges.
Not clear to me yet whether that does anything for my Sudoku predicament -- it miiiight have utility? -- but it certainly is A Thing That Is True.
Which, thinking about it for a minute, makes sense: each connection between two nodes on this graph is an odd to an even or vice versa. Which!
If node A is odd and it connects to node B, node B must be even. (Or else it'd be odd + odd, giving us an even number greater than 2, hence not prime.)
And if B is even, any node C it connects to must in turn be odd.
But now our node A and node C have the same parity: they're both odd, and so add to an even value, which wouldn't be prime.
In retrospect, actually pretty obvious, but it's fun to have it click into place from a totally different visual direction.
@joshmillard posts like this give me endless screaming brain
@scream thank you, my thoughts exactly lol
I love reading things by people who know so much about things I don't, its a bit of a treasure here
Josh "cortex" Millard
TeflonTrout 
he/him
Endless Screaming
James Young