Paper day for least-model-dependent astrophysics! On today's menu: an old-new mathem. robust galaxy clustering, a clever way to reduce large distance-uncertainties from non-redshift probes & our favourite friendly neighbouring cluster, Coma! 🧶🧶
https://arxiv.org/abs/2504.04135
#astronomy #astrophysics #cosmology #cosmicflows4 #DarkMatter #DarkEnergy

Unveiling the Coma Cluster Structure: From the Core to the Hubble Flow
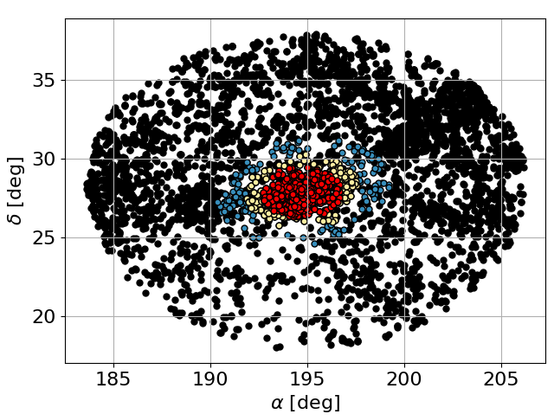
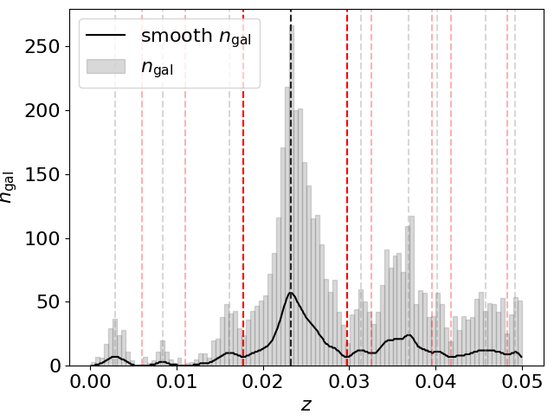
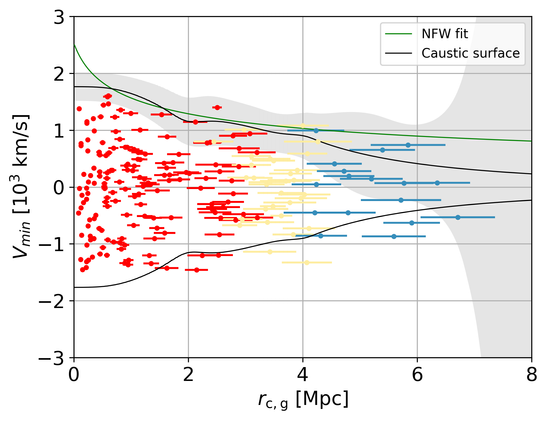
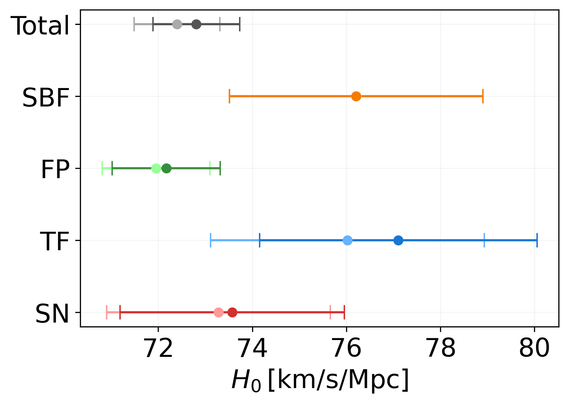
The Coma cluster, embedded in a cosmic filament, is a complex and dynamically active structure in the local Universe. Applying a density-based member selection (dbscan) to data from the Sloan Digital Sky Survey (SDSS), we identify its virilised core and zero-velocity boundary. Cross-correlating with the Cosmicflows-4 (CF4) catalogue enables a velocity-distance analysis, incorporating radial infall models and redshift-independent distance estimators. This reveals, for the first time, the Hubble flow surrounding Coma, a first step to investigate the entanglement between the dark matter in bound objects and the dark energy driving the expansion of their surroundings. The distance to the Coma centre is determined as $69.959 \pm 0.012 \, h^{-1}~\text{Mpc}$. From dbscan, we infer a virial radius of $r_{\rm vir} = \left(1.95 \pm 0.12\right)\,h^{-1}~\text{Mpc}$ and a turnaround of $r_{\rm ta} \geq 4.87~{h}^{-1}~\mbox{Mpc}$. Combining the SDSS redshifts with the CF4 distances, we estimate the Hubble constant to be $H_0 = (73.10 \pm 0.92)~\mbox{km}/\mbox{s}/\mbox{Mpc}$. However, with different calibrations for the distance moduli, $H_0$ varies between $[72, 80]$ km/s/Mpc. Mass estimates via caustics, the virial theorem, and the Hubble-flow method yield $M = [0.77, 2.0] \times 10^{15}\,h^{-1}\,M_{\odot}$, consistent with prior studies. Our systematic approach maps the structure of Coma into the local Hubble flow and shows the degeneracies between dynamical parameters such as the Hubble constant, the virial radius, and the total mass.