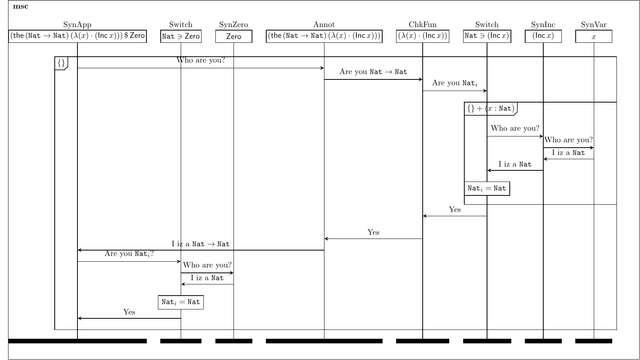
Typing derivations are great at *showing* the result of type checking.

Derivations are not so great at showing the communication structure.

Given a bidirectional account of the STLC with Nat (Zero and Inc) with term level annotations.

For my 101, I was thinking of showing the derivation for:

\(
(\mathsf{the}\,(\mathtt{Nat}\rightarrow\mathtt{Nat})\,(\lambda{(x)\cdot(\mathsf{Inc}\,x))})\,\$\,\mathsf{Zero}
\)

As the attached MSC chart. (Not yet worked out how to squeeze in context growth and equality checks)

Diagram might be too much change.

I have experimented with a graph representation but let us stick to standardised notation ;-)