The 12th root of 2 times the 7th root of 5 is
1.333333192495....
And since the numbers 5, 7, and 12 show up in scales, this weird fact has implications for music! It leads to a remarkable meta-meta-glitch in tuning systems. Let's check it out.
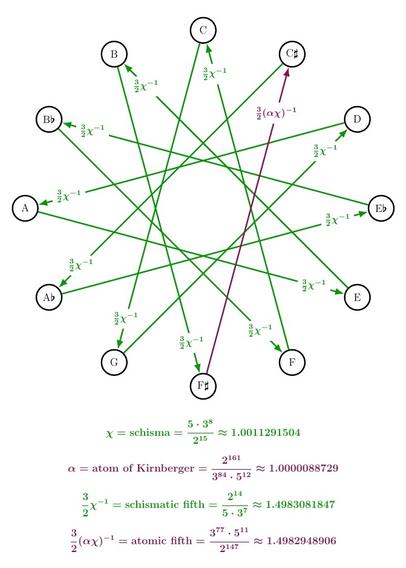
Two important glitches that afflict tuning systems are the Pythagorean comma and the syntonic comma. If you go up 12 fifths, multiplying the frequency by 3/2 each time, you go up a bit less than 7 octaves. The ratio is the "Pythagorean comma":
p = 531441/524288 ≈ 1.01364326477
And if you go up four fifths, you go up a bit more than 2 octaves and a major third (which ideally has a frequency ratio of 5/4). The ratio is the "syntonic comma":
σ = 81/80 = 1.0125
In music it would be very convenient if these two glitches were the same - and sometimes musicians pretend they are. But they're not! So their ratio is a tiny meta-glitch. It's called the "schisma":
χ = p/σ = 32805/32768 ≈ 1.0011298906
and it was discovered by an advisor to the Gothic king Theodoric the Great.
In the most widely used tuning system today, a fifth is not 3/2 but slightly less: it's
2^(7/12) ≈ 1.4983070769
The ratio of 3/2 and this slightly smaller fifth is called the "grad":
γ = p^(1/12) ≈ 1.0011291504
Look! The grad is amazingly close to the schisma! They agree to 7 decimal places! Their ratio is a meta-meta-glitch called the "Kirnberger kernel":
χ/γ ≈ 1.0000007394
If you unravel the mathematical coincidence that makes this happens, you'll see it boils down to
2^(1/12) 5^(1/7) ≈ 1.333333192495
being very close to 4/3. And this coincidence let Bach's students Johann Kirnberger invent an amazing tuning system.
(1/2)