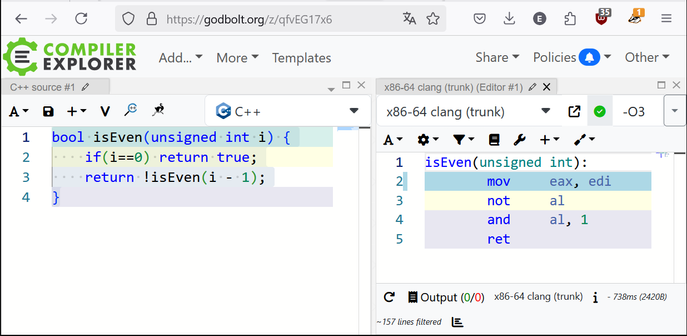
@ela This is quite impressive, and I wonder how complex you could make these kinds of functions while still having this kind of optimisation happening.
But it does make me ask: Should perhaps the compiler warn about these cases? I mean, it's great that the compiler can optimise it, but when it can, the code should probably be simplified, and that would be better than relying on the compiler.
@loke The problem here is that the compiler can't tell if something is just an idiomatic expression or bad coding. In fact, such warnings might even distract programmers from getting things right.
It's very important to keep in mind that source code has a dual purpose. Yes, it instructs the computer what to do, but computers are perfectly fine with machine instructions. Much more importantly, source code exists for humans to read, understand and reason about.
Premature optimization is the root of all evil. The primary goals of writing code must be correctness and readability, with correctness often being influenced by readability.
Sure, some code needs to be super fast. Your interrupt handler for that 10GB network card? This code doing the task switching in your OS? Absolutely. Every cycle counts. But in order to achieve this, you need to measure. I've seen a lot of theories about performance improvements collide hard with the realities of modern CPU and compiler architecture. Always profile, always measure, always benchmark.
And for that precious lines of code, modern compilers are happy to infodump on you every step they take.
@ela @loke There's a lot of examples of this. Like mergesort vs quicksort (yes, no one uses vanilla quicksort but I would argue that it's closer to quick than merge). And then in network science you have these algorithms where runtime is around cubic and whether quadratic, cubic or tertiary is the right choice very much depends on the properties of your graph, like actual size, rather than what happens when n goes towards infinite.
Edit: urgh, I'm being a reply guy. Sorry. Graphs are neat.
I would expect that this is the combination of a few things:
First, the compiler will turn a tail-recursive function into a loop. This is a fairly trivial transform (Python explicitly prohibits it because it loses backtrace information)l it’s just replacing the tail call with a branch to the entry point.
After that, you have a simple loop. There will be a bit of canonicalisation to make it easier to analyse.
My guess is that this would then be handled by scalar evolution, which tries to model outputs from the loop as polynomials computed from the induction variable. Note that the loop has no side effects. This means each value in each iteration can be calculated from the previous one, which means that there must be a function that goes from the induction variable to the input to the output, so you’re just solving for that.
This particular case might be simpler because the value at the end depends on a single bit in the input, so it might be that known-bits analysis gives you the answer.
If you pass -mllvm -print-after-all to Clang, it will print the LLVM IR after each pass has run, so you can see all of the intermediate steps.
First, the compiler will turn a tail-recursive function into a loop.
so is the implication here that the compiler would also recognize this non-tailrec example above and transform it to tailrec first?
Ela
Elias Mårtenson
Morten Grøftehauge
David Chisnall (*Now with 50% more sarcasm!*)
soft